Aufgabentypen: Unterschied zwischen den Versionen
| (78 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Zur Etablierung einer lernförderlichen [[Aufgabengestaltung|Aufgabenkultur]] | Zur Etablierung einer lernförderlichen [[Aufgabengestaltung|Aufgabenkultur]] im Mathematikunterricht sollte der Einsatz verschiedener Aufgabentypen in der Unterrichtskonzeption berücksichtigt werden. Hierbei spielen die ''Aufgabentypen nach Bruder'' eine tragende Rolle, da durch sie eine Variabilität des Unterrichts garantiert werden kann, welche eine kognitive Anregung der Schülerinnen und Schüler gewährleistet. <ref>Bruder, R.(2000): Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung - Wege zu einem anspruchsvollen Mathematikunterricht für alle. In: Flade & Herget (Hrsg.): Mathematik lehren und lernen nach TIMSS. Anregungen für die Sekundarstufen. Berlin: Volk und Wissen. ISBN 3060023654.</ref> | ||
<br />Eine motivierende und lernfördernde Aufgabenkultur im Mathematikunterricht sollte außerdem ''differenzierende'', ''prozessorientierte'' und ''diagnostische'' Aufgaben beinhalten. Diese werden im Folgenden vorgestellt. <ref>Leuders, T. (2018): Mathematik Didaktik. Praxishandbuch für die Sekundarstufe I und II. Berlin: Cornselsen Verlag Scripor GmbH&Co. KG. S. 300ff. ISBN 3589216956</ref> | |||
[[Datei:Spannender Unterricht.png|thumb| Karikatur von Michael Hüter <ref>Karikatur von Michael Hüter aufgerufen unter: https://docplayer.org/docs-images/66/55548085/images/10-1.jpg Stand: 01.09.2020</ref>]] | [[Datei:Spannender Unterricht.png|thumb| Karikatur von Michael Hüter <ref>Karikatur von Michael Hüter aufgerufen unter: https://docplayer.org/docs-images/66/55548085/images/10-1.jpg Stand: 01.09.2020</ref>]] | ||
==Relevanz== | ==Relevanz== | ||
Die Relevanz zur Weiterentwicklung der Aufgabenkultur lässt sich in empirischen Untersuchungen der letzten Jahre wiederfinden. Gemeinsame Ursachen für auftretende Phänomene ist auf eine unzureichend ausgeprägte Aufgabenkultur im Mathematikunterricht deutscher Schulen zurückzuführen. | Die Relevanz zur Weiterentwicklung der Aufgabenkultur lässt sich in empirischen Untersuchungen der letzten Jahre wiederfinden. Gemeinsame Ursachen für auftretende Phänomene ist auf eine unzureichend ausgeprägte Aufgabenkultur im Mathematikunterricht deutscher Schulen zurückzuführen. <ref>Bruder, R. (2006): Modul 1: Weiterentwicklung der Aufgabenkultur im Mathematikunterricht. Aufgerufen auf: http://www.sinus-transfer.de/fileadmin/MaterialienBT/Bruder_Modul1.pdf Stand: 02.09.2020</ref> | ||
<br />Exemplarische Beispiele werden im Folgenden genannt: | <br />Exemplarische Beispiele werden im Folgenden genannt: | ||
*Lernende aus Deutschland weisen in der [[PISA-Studie]] 2003 deutlich höhere Werte im Bereich der Problemlösefähigkeiten im Vergleich zu der mathematischen Kompetenz auf. Diesen Befund weisen nur sehr wenige Staaten im internationalen Vergleich auf. | *Lernende aus Deutschland weisen in der [[PISA-Studie]] 2003 deutlich höhere Werte im Bereich der Problemlösefähigkeiten im Vergleich zu der mathematischen Kompetenz auf. Diesen Befund weisen nur sehr wenige Staaten im internationalen Vergleich auf. Interpretativ bedeutet dies, dass das kognitive Potenzial deutscher Schülerinnen und Schüler weniger erfolgreich in mathematische Kompetenz umgesetzt wird. <ref>PISA 2003, Ergebnisse des zweiten Internationalen Vergleichs, Zusammenfassung unter: http://archiv.ipn.uni-kiel.de/PISA/PISA2003_E_Zusammenfassung.pdf, S.18 </ref> | ||
*Die [[ | *Die [[TIMS-Studie]] weist auf, dass im Mathematikunterricht an deutschen Schulen komplexe Aufgaben am wenigsten gestellt werden, im Vergleich zu den USA und Japan. <ref> vgl. Neubrand, J. (2002): Eine Klassifikation mathematischer Aufgaben zur Analyse von Unterrichtssituationen. Selbsttätiges Arbeiten in Schülerarbeitsphasen in den Stunden der TIMSS-Video-Studie. Hildesheim/Berlin: Franzbecker. ISBN 3881203443 </ref> | ||
*Inhaltliches mathematisches Denken von Lernenden der Klassenstufen 5 und 6 werden durch die Anwendung erlernter kalkülhafter Regeln ersetzt. <ref>Pekrun, R.; Götz, T.; vom Hofe, R.; Blum, W.; Jullien, S.; Zirngibl, A.; Kleine, M.; Wartha, S.; Jordan, A. (2004): Emotionen und Leistung im Fach Mathematik: Ziele und erste Befunde aus dem „Projekt zur Analyse der Leistungsentwicklung in Mathematik“ (PALMA), Münster: Waxmann, S.359, ISBN 3830913990 </ref> | *Inhaltliches mathematisches Denken von Lernenden der Klassenstufen 5 und 6 werden durch die Anwendung erlernter kalkülhafter Regeln ersetzt. <ref>Pekrun, R.; Götz, T.; vom Hofe, R.; Blum, W.; Jullien, S.; Zirngibl, A.; Kleine, M.; Wartha, S.; Jordan, A. (2004): Emotionen und Leistung im Fach Mathematik: Ziele und erste Befunde aus dem „Projekt zur Analyse der Leistungsentwicklung in Mathematik“ (PALMA), Münster: Waxmann, S.359, ISBN 3830913990 </ref> | ||
Die genannten empirischen Phänomene weisen keineswegs eine geringere Leistungsfähigkeit deutscher Schülerinnen und Schüler im internationalen Vergleich auf. Es besteht allerdings grundlegender Bedarf diese Leistungsfähigkeit im Mathematikunterricht abzurufen. Dabei sollte unter anderem die Entwicklung | Die genannten empirischen Phänomene weisen keineswegs eine geringere Leistungsfähigkeit deutscher Schülerinnen und Schüler im internationalen Vergleich auf. Es besteht allerdings grundlegender Bedarf diese Leistungsfähigkeit im Mathematikunterricht abzurufen. Dabei sollte unter anderem die Entwicklung einer lernförderlichen Aufgabenkultur eine zentrale Rolle spielen. <ref>Bruder, R. (2006): Modul 1: Weiterentwicklung der Aufgabenkultur im Mathematikunterricht. Aufgerufen auf: http://www.sinus-transfer.de/fileadmin/MaterialienBT/Bruder_Modul1.pdf Stand: 02.09.2020</ref> | ||
<br /> Im Folgenden werden Möglichkeiten zur Umsetzung dieses Ziels dargestellt. | <br /> Im Folgenden werden Möglichkeiten zur Umsetzung dieses Ziels dargestellt. | ||
==Aufgabentypen nach Bruder== | ==Aufgabentypen nach Bruder== | ||
[[Datei:Aufgabentypen Bruder.png|thumb|Aufgabentypen nach Bruder (2000)<ref>Bruder, R.(2000): Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung - Wege zu einem anspruchsvollen Mathematikunterricht für alle. | [[Datei:Aufgabentypen Bruder.png|thumb|'''Aufgabentypen''' nach Bruder (2000)<ref>Bruder, R.(2000): Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung - Wege zu einem anspruchsvollen Mathematikunterricht für alle. In: Flade & Herget (Hrsg.): Mathematik lehren und lernen nach TIMSS. Anregungen für die Sekundarstufen. Berlin: Volk und Wissen. ISBN 3060023654. Aufgerufen auf: https://slideplayer.org/slide/11869083/ Stand: 02.09.2020</ref> ]] | ||
Diese Aufgabentypen | Die Mathematikdidaktikerin Regina Bruder hat sich im Zuge der Diskussion zur Verbesserung der Unterrichtskultur, als Folge der Evaluation der [[TIMS-Studie]], damit auseinandergesetzt, "wie es gelingen kann, dass sich Schüler_innen erfolgreicher als bisher mit nicht (schematisch) eingeübten Aufgaben auseinandersetzen wollen und können. Im Unterrichtsalltag ist die Verführung groß, sich auf bestimmte Standardaufgaben zurückzuziehen, die systematisch trainiert werden." <ref>Bruder, R.(2000): Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung - Wege zu einem anspruchsvollen Mathematikunterricht für alle. In: Flade & Herget (Hrsg.): Mathematik lehren und lernen nach TIMSs. Anregungen für die Sekundarstufen. Berlin: Volk und Wissen. ISBN 3060023654</ref> Bruder definiert Aufgaben als ''"Aufforderungen zum Lernhandeln"'' <ref>Bruder, R.(2000): Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung - Wege zu einem anspruchsvollen Mathematikunterricht für alle. In: Flade & Herget (Hrsg.): Mathematik lehren und lernen nach TIMSS. Anregungen für die Sekundarstufen. Berlin: Volk und Wissen. ISBN 3060023654</ref> und klassifiziert acht mögliche Aufgabentypen anhand drei verschiedener Komponenten: | ||
<ref>Bruder, R.(2000): Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung - Wege zu einem anspruchsvollen Mathematikunterricht für alle. | *'''Anfangssituation''' (Gegebenes) | ||
*'''Transformation''' (Lösungsweg) | |||
*'''Endsituation''' (Gesuchtes) | |||
Durch die Variation der Belegung der Komponenten entstehen acht unterschiedliche Aufgabentypen, die in der seitlichen Grafik aufgeführt sind. Laut Bruder ermöglicht die Aufgabentypisierung die Evaluierung des eigenen Unterrichts. Dies ermöglicht es Lehrpersonen zu erkennen wie vielseitig oder auch "verkopft" der eigene Unterricht ist. Zur Umsetzung einer lernförderlichen Aufgabenkultur ist eine Ausgewogenheit der verschiedenen Aufgabentypen konstituierend. | |||
Bruder geht sogar soweit und behauptet: | |||
::''"Wenn diese Aufgabentypen im Unterricht nicht in angemessenen Anteilen (das bedeutet keineswegs gleich-gewichtig!) vorkommen, haben viele SchülerInnen kaum reale Chancen, fundamentale Ideen der Mathematik und Wege und Möglichkeiten für Anwendungen von Mathematik zu erfahren und zu verstehen." <ref>Bruder, R.(2000): Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung - Wege zu einem anspruchsvollen Mathematikunterricht für alle. In: Flade & Herget (Hrsg.): Mathematik lehren und lernen nach TIMSS. Anregungen für die Sekundarstufen. Berlin: Volk und Wissen. ISBN 3060023654</ref>'' | |||
Diese Aufgabentypen garantieren demnach eine kognitive Aktivierung der Schülerinnen und Schüler, indem wesentliche Lerntätigkeiten abgebildet, vernetzendes Denken ermöglicht, individuelle Freiräume zur Differenzierung dargeboten und methodische Variabilität des Unterrichts zur Motivationssteigerung eingefordert werden. | |||
<ref>Bruder, R.(2000): Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung - Wege zu einem anspruchsvollen Mathematikunterricht für alle. In: Flade & Herget (Hrsg.): Mathematik lehren und lernen nach TIMSS. Anregungen für die Sekundarstufen. Berlin: Volk und Wissen. ISBN 3060023654</ref> | |||
==Differenzierende Aufgaben== | ==Differenzierende Aufgaben== | ||
Differenzierende Aufgaben berücksichtigen in besonderem Maße unterschiedliche Niveaustufen der Lernenden, sodass Aufgaben je nach individuellem Vorwissen und Leistungsstand bearbeitet werden können. Eckpfeiler | Differenzierende Aufgaben berücksichtigen in besonderem Maße unterschiedliche Niveaustufen der Lernenden, sodass Aufgaben je nach individuellem Vorwissen und Leistungsstand bearbeitet werden können. Eckpfeiler differenzierenden Unterrichts sind: | ||
*'''Sicherung des Ausgangsniveaus''' (zum Beispiel durch vermischte Kopfübungen) | *'''Sicherung des Ausgangsniveaus''' (zum Beispiel durch vermischte Kopfübungen) | ||
*'''Ziel- und Inhaltstransparenz''' (zum Beispiel durch Lernprotokolle) | *'''Ziel- und Inhaltstransparenz''' (zum Beispiel durch Lernprotokolle) | ||
*'''Förderung der Selbstregulation''' (zum Beispiel durch Checklisten zur Klausurvorbereitung) | *'''Förderung der Selbstregulation''' (zum Beispiel durch Checklisten zur Klausurvorbereitung) | ||
*'''kognitive Aktivierung''' (zum Beispiel durch angepasste Anforderungen an verschiedene Lernvoraussetzungen) <ref>Roder, U. & Bruder, R. (2015): MAKOS – Ein Projekt zur Umsetzung der Abiturstandards Mathematik in Hessen. In G. Kaiser & H.-W. Henn (Hrsg.), Werner Blum und seine Beiträge zum Modellieren. Festschrift zum 70. Geburtstag. Wiesbaden: Springer Spektrum Verlag. S. 284 </ref> | *'''kognitive Aktivierung''' (zum Beispiel durch angepasste Anforderungen an verschiedene Lernvoraussetzungen) <ref>Roder, U. & Bruder, R. (2015): MAKOS – Ein Projekt zur Umsetzung der Abiturstandards Mathematik in Hessen. In G. Kaiser & H.-W. Henn (Hrsg.), Werner Blum und seine Beiträge zum Modellieren. Festschrift zum 70. Geburtstag. Wiesbaden: Springer Spektrum Verlag. S. 284 ISBN 9783658095314</ref> | ||
Im Folgenden werden verschiedene Beispiele für differenzierende aufgabenbezogene Methoden vorgestellt. | |||
<br />Siehe auch: [[Binnendifferenzierung]] | |||
===Optionale Teilaufgaben=== | ===Optionale Teilaufgaben=== | ||
| Zeile 30: | Zeile 41: | ||
===Blütenaufgaben=== | ===Blütenaufgaben=== | ||
[[Datei:Blütenaufgabe2.png|thumb|Beide Grundaufgaben sind zu bearbeiten. Beim Aufstieg der Blüte bestehen Wahlmöglichkeiten. <ref>Storz, R. (2014): Mathematik differenziert und individualisiert unterrichten. Hallbergmoos: Aulis Verlag. S. 143 ISBN 9783761429266 </ref>]] | [[Datei:Blütenaufgabe2.png|thumb|Visualisierung des typischen Aufbaus einer '''Blütenaufgabe'''. <br/ >Beide Grundaufgaben sind zu bearbeiten. Beim Aufstieg der Blüte bestehen Wahlmöglichkeiten. <ref>Storz, R. (2014): Mathematik differenziert und individualisiert unterrichten. Hallbergmoos: Aulis Verlag. S. 143 ISBN 9783761429266 </ref>]] | ||
Blütenaufgaben sind | Blütenaufgaben sind anforderungsgestufte Aufgaben, bestehend aus mehreren Teilaufgaben mit zunehmendem Anspruchsniveau zum selben Themenkontext. | ||
Blütenaufgaben beginnen mit einer geschlossenen Einstiegsaufgabe, die den Schülerinnen und Schüler zugänglich ist. Es folgen weitere offene Teilaufgaben mit gestuften Anforderungen. | Blütenaufgaben beginnen mit einer geschlossenen Einstiegsaufgabe, die den Schülerinnen und Schüler zugänglich ist. Es folgen weitere offene Teilaufgaben mit gestuften Anforderungen. | ||
Dieser Aufgabentyp ermöglicht, dass mit einer einzigen Aufgabe Grundanforderungen gestellt und weiterführende Anforderungen geöffnet werden können. <ref>Zeitler, H. (2013): In der Vielfalt liegt die Stärke - Handreichung zur Individualisierung des Lernens für die gesellschaftswissenschaftlichen Fächer. Berlin: Ruksaldruck GmbH, S.17f ISBN 9783944541020</ref> <ref>Storz, R. (2014): Mathematik differenziert und individualisiert unterrichten. Hallbergmoos: Aulis Verlag. S. 142ff ISBN 9783761429266 </ref> | Dieser Aufgabentyp ermöglicht, dass mit einer einzigen Aufgabe Grundanforderungen gestellt und weiterführende Anforderungen geöffnet werden können. <ref>Zeitler, H. (2013): In der Vielfalt liegt die Stärke - Handreichung zur Individualisierung des Lernens für die gesellschaftswissenschaftlichen Fächer. Berlin: Ruksaldruck GmbH, S.17f ISBN 9783944541020</ref> <ref>Storz, R. (2014): Mathematik differenziert und individualisiert unterrichten. Hallbergmoos: Aulis Verlag. S. 142ff ISBN 9783761429266 </ref> | ||
===Aufgabensets=== | ===Aufgabensets=== | ||
Ein Aufgabenset | Ein Aufgabenset beinhaltet circa zehn schwierigkeitsgestufte Aufgaben zu einem Thema aus dem (inner-)mathematischen Kontext, welche gezielt für eine einzelne Übungsphase zusammengestellt werden. Dabei bearbeitet die einzelne Schülerin bzw. der einzelne Schüler nicht alle zehn Aufgaben, sondern nur eine bestimmte Anzahl der vorgegebenen Aufgaben. Die ersten Aufgaben bewegen sich im Anforderungsbereich I und beinhalten hauptsächlich Grundaufgaben und Aufgabenumkehrungen. Die nächsten Aufgaben sind dem Anforderungsbereich II zuzuordnen und beinhalten Anwendungen oder erste Verallgmeinerungen. Die letzten Aufgaben sind dem dritten Anforderungsbereich zuzuordnen. Hierbei werden vertiefende Transferaufgaben behandelt. Die Zusammenstellung der Inhalte und die Wahlmöglichkeiten gewährleisten, dass die Lernenden entsprechend ihres Festigungsbedarfs und ihres Leistungsvermögens angemessen gefördert und gefordert werden. <ref>Roder, U. & Bruder, R. (2015): MAKOS – Ein Projekt zur Umsetzung der Abiturstandards Mathematik in Hessen. In G. Kaiser & H.-W. Henn (Hrsg.), Werner Blum und seine Beiträge zum Modellieren. Festschrift zum 70. Geburtstag. Wiesbaden: Springer Spektrum Verlag. S. 290. ISBN 9783658095314</ref> | ||
==Prozessorientierte Aufgaben== | ==Prozessorientierte Aufgaben== | ||
[[Datei:Modellierungskreislauf.png|thumb|Visualisierung des '''Modellierungskreislaufs''' nach Blum & Leiß (2005). <ref>Blum, W. & Leiß, D. (2005): Modellieren im Unterricht mit der “Tanken”-Aufgabe, In: Mathematik lehren, H. 128, Feb. 2005, S. 19. Hannover: Friedrich Verlag</ref>]] | |||
Prozessorientierte Aufgaben konzentrieren sich auf die anzuwendenden Prozesse des Problemlösens oder Modellierens. Die Kenntnisse von mathematischen Inhalten rückt hierbei eher in den Hintergrund. | Prozessorientierte Aufgaben konzentrieren sich auf die anzuwendenden Prozesse des Problemlösens oder Modellierens. Die Kenntnisse von mathematischen Inhalten rückt hierbei eher in den Hintergrund. | ||
<br />Ein Beispiel prozessorientierter Aufgaben im Mathematikunterricht sind '''Modellierungsaufgaben'''. Die Kompetenz des Modellierens beinhaltet „realitätsbezogene Situationen durch den Einsatz mathematischer Mittel zu verstehen, zu strukturieren und das der Situation zugrunde liegende Problem einer Lösung zuzuführen sowie Mathematik in der Realität zu erkennen und zu beurteilen.“ <ref>Leiß, D., & Blum, W. (2006): Beschreibung zentraler mathematischer Kompetenzen. In: W. Blum, C. Drüke-Noe, R. Hartung, & O. Köller (Hrsg.): Die Bildungsstandards Mathematik (S. 33–50). Berlin: Cornelsen Scriptor. S. 41f</ref> | |||
=== | ===Phasen und Ziele von Modellierungsaufgaben=== | ||
Die verschiedenen Phasen eines Modellierungsprozesses sind in der seitlich aufgeführten Grafik visualisiert. Die von den Schülerinnen und Schülern zu vollzuiehenden Teilschritte sind folgende: | |||
# ''Verstehen:'' Aufgabenstellung verstehen und Situationsmodell bilden | |||
# ''Vereinfachen/ Strukturieren:'' Durch Treffen geeigneter Annahmen wird das Situationsmodell strukturiert, idealisiert und präzisiert sowie ein Realmodell konstruiert | |||
# ''Mathematisieren:'' Das Realmodell wird in ein mathematisches Modell transformiert | |||
# ''Mathematisch arbeiten:'' Ein ausgewähltes mathematisches Verfahren wird angewendet und ein mathematisches Resultat hergeleitet | |||
# ''Interpretieren:'' Das mathematische Resultat wird interpretiert und in ein reales Resultat transformiert | |||
# ''Validieren:'' Dieses reale Resultat wird unter der Gegebenheiten der Situation überprüft | |||
# ''Vermitteln:'' Der Lösungsprozess wird nachvollziehbar dokumentiert <ref>Achmetli, K., Krug, A., Schukajlow,S. (2015): Multiple Lösungsmöglichkeiten und ihre Nutzung beim mathematischen Modellieren. In: G. Kaiser & H.-W. Henn (Hrsg.), Werner Blum und seine Beiträge zum Modellieren. Festschrift zum 70. Geburtstag. Wiesbaden: Springer Spektrum Verlag. S. 26 ISBN 9783658095314</ref> | |||
Durch den Einsatz und die Anwendung von Modellierungsaufgaben im Unterricht werden '''inhaltsorientierte''' (Erschließung der realen Welt mit mathematischen Mitteln), '''prozessbezogene''' (Ausbildung mathematischer Problemlösefähigkeiten, wie zum Beispiel heuristischer Strategien) und '''allgemeine Ziele ''' (kulturbezogene Vermittlung von der Verwendung der Mathematik in der realen Welt, als zentraler Aspekt für die Entwicklung der Mathematik als Wissenschaft, dazu zählt auch die kritische Reflexion mathematischer Modelle in der Gesellschaft) verfolgt. <ref>Ferri, R., Greefrath, G., Kaiser, G. (2013): Mathematisches Modellieren für Schule und Hochschule. Wiesbaden: Springer Spektrum. S. 20</ref> | |||
==Diagnoseaufgaben== | ==Diagnoseaufgaben== | ||
Diagnoseaufgaben sind ein mögliches Werkzeug Erkenntnisse über den aktuellen Wissensstand und vorhandene mathematische Problemlösefähigkeiten der Lernenden in Erfahrung zu bringen. Sie können außerdem Hinweise darauf geben worin genau Kenntnisdefizite beim Verständnis mathematischer Sachverhalte vorhanden sind. Dies ist insbesondere für die Bereitstellung individueller Förderangebote von großer Bedeutung. | Diagnoseaufgaben sind ein mögliches Werkzeug, Erkenntnisse über den aktuellen Wissensstand und vorhandene mathematische Problemlösefähigkeiten der Lernenden in Erfahrung zu bringen. Sie können außerdem Hinweise darauf geben, worin genau Kenntnisdefizite beim Verständnis mathematischer Sachverhalte vorhanden sind. Dies ist insbesondere für die Bereitstellung individueller Förderangebote von großer Bedeutung. | ||
<br />Diagnoseaufgaben sollten bestimmte Bedingungen erfüllen: | <br />Diagnoseaufgaben sollten bestimmte Bedingungen erfüllen: | ||
*Relation zwischen entstehenden Schülerlösungen und systematischen Fehlerstrategien | *Sie sollten eine erkennbare '''Relation''' zwischen entstehenden '''Schülerlösungen''' und systematischen '''Fehlerstrategien''' herstellen können. Dies dient der Vergleichbarkeit der entstehenden Ergebnisse und somit der qualitativen Einschätzung dieser. | ||
*Lösungswege | *Um eine detaillierte Fehlerstrategieanalyse zu ermöglichen sollten die '''Lösungswege''' der Schülerinnen und Schüler begründet dargelegt werden. | ||
*von | *Um bei der Anwendung von Diagnoseaufgaben die Erhebung des Umgangs mit Zeit- und Leistungsdruck auszuschließen, sollten Diagnoseaufgaben '''von Leistungsbewertungen entkoppelt''' sein. | ||
*langfristig | *Leistungsstanddiagnosen sollten '''langfristig''', hinsichtlich bestimmter Variablen, angelegt sein, um eine möglichst vielsietige und fundiert Diagnose zu gewährleisten. | ||
* | *Für den Vergleich des Lernendenselbstkozenpts mit dem tatsächlichen Lernstand sollte eine '''Selbsteinschätzung''' oder eine '''Reflexion''' in der Diagnose des Leistungsstands implementiert sein. <ref>Leuders, T. (2018): Mathematik Didaktik. Praxishandbuch für die Sekundarstufe I und II. Berlin: Cornselsen Verlag Scripor GmbH&Co. KG. S. 302f. ISBN 3589216956</ref> | ||
==Einzelnachweise== | ==Einzelnachweise== | ||
<references /> | <references /> | ||
[[Kategorie: Theorie]] | [[Kategorie: Theorie]] | ||
Aktuelle Version vom 10. September 2020, 09:06 Uhr
Zur Etablierung einer lernförderlichen Aufgabenkultur im Mathematikunterricht sollte der Einsatz verschiedener Aufgabentypen in der Unterrichtskonzeption berücksichtigt werden. Hierbei spielen die Aufgabentypen nach Bruder eine tragende Rolle, da durch sie eine Variabilität des Unterrichts garantiert werden kann, welche eine kognitive Anregung der Schülerinnen und Schüler gewährleistet. [1]
Eine motivierende und lernfördernde Aufgabenkultur im Mathematikunterricht sollte außerdem differenzierende, prozessorientierte und diagnostische Aufgaben beinhalten. Diese werden im Folgenden vorgestellt. [2]

Relevanz
Die Relevanz zur Weiterentwicklung der Aufgabenkultur lässt sich in empirischen Untersuchungen der letzten Jahre wiederfinden. Gemeinsame Ursachen für auftretende Phänomene ist auf eine unzureichend ausgeprägte Aufgabenkultur im Mathematikunterricht deutscher Schulen zurückzuführen. [4]
Exemplarische Beispiele werden im Folgenden genannt:
- Lernende aus Deutschland weisen in der PISA-Studie 2003 deutlich höhere Werte im Bereich der Problemlösefähigkeiten im Vergleich zu der mathematischen Kompetenz auf. Diesen Befund weisen nur sehr wenige Staaten im internationalen Vergleich auf. Interpretativ bedeutet dies, dass das kognitive Potenzial deutscher Schülerinnen und Schüler weniger erfolgreich in mathematische Kompetenz umgesetzt wird. [5]
- Die TIMS-Studie weist auf, dass im Mathematikunterricht an deutschen Schulen komplexe Aufgaben am wenigsten gestellt werden, im Vergleich zu den USA und Japan. [6]
- Inhaltliches mathematisches Denken von Lernenden der Klassenstufen 5 und 6 werden durch die Anwendung erlernter kalkülhafter Regeln ersetzt. [7]
Die genannten empirischen Phänomene weisen keineswegs eine geringere Leistungsfähigkeit deutscher Schülerinnen und Schüler im internationalen Vergleich auf. Es besteht allerdings grundlegender Bedarf diese Leistungsfähigkeit im Mathematikunterricht abzurufen. Dabei sollte unter anderem die Entwicklung einer lernförderlichen Aufgabenkultur eine zentrale Rolle spielen. [8]
Im Folgenden werden Möglichkeiten zur Umsetzung dieses Ziels dargestellt.
Aufgabentypen nach Bruder
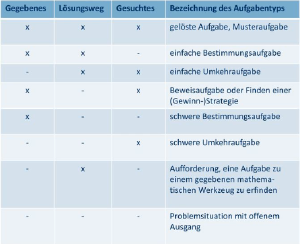
Die Mathematikdidaktikerin Regina Bruder hat sich im Zuge der Diskussion zur Verbesserung der Unterrichtskultur, als Folge der Evaluation der TIMS-Studie, damit auseinandergesetzt, "wie es gelingen kann, dass sich Schüler_innen erfolgreicher als bisher mit nicht (schematisch) eingeübten Aufgaben auseinandersetzen wollen und können. Im Unterrichtsalltag ist die Verführung groß, sich auf bestimmte Standardaufgaben zurückzuziehen, die systematisch trainiert werden." [10] Bruder definiert Aufgaben als "Aufforderungen zum Lernhandeln" [11] und klassifiziert acht mögliche Aufgabentypen anhand drei verschiedener Komponenten:
- Anfangssituation (Gegebenes)
- Transformation (Lösungsweg)
- Endsituation (Gesuchtes)
Durch die Variation der Belegung der Komponenten entstehen acht unterschiedliche Aufgabentypen, die in der seitlichen Grafik aufgeführt sind. Laut Bruder ermöglicht die Aufgabentypisierung die Evaluierung des eigenen Unterrichts. Dies ermöglicht es Lehrpersonen zu erkennen wie vielseitig oder auch "verkopft" der eigene Unterricht ist. Zur Umsetzung einer lernförderlichen Aufgabenkultur ist eine Ausgewogenheit der verschiedenen Aufgabentypen konstituierend. Bruder geht sogar soweit und behauptet:
- "Wenn diese Aufgabentypen im Unterricht nicht in angemessenen Anteilen (das bedeutet keineswegs gleich-gewichtig!) vorkommen, haben viele SchülerInnen kaum reale Chancen, fundamentale Ideen der Mathematik und Wege und Möglichkeiten für Anwendungen von Mathematik zu erfahren und zu verstehen." [12]
Diese Aufgabentypen garantieren demnach eine kognitive Aktivierung der Schülerinnen und Schüler, indem wesentliche Lerntätigkeiten abgebildet, vernetzendes Denken ermöglicht, individuelle Freiräume zur Differenzierung dargeboten und methodische Variabilität des Unterrichts zur Motivationssteigerung eingefordert werden. [13]
Differenzierende Aufgaben
Differenzierende Aufgaben berücksichtigen in besonderem Maße unterschiedliche Niveaustufen der Lernenden, sodass Aufgaben je nach individuellem Vorwissen und Leistungsstand bearbeitet werden können. Eckpfeiler differenzierenden Unterrichts sind:
- Sicherung des Ausgangsniveaus (zum Beispiel durch vermischte Kopfübungen)
- Ziel- und Inhaltstransparenz (zum Beispiel durch Lernprotokolle)
- Förderung der Selbstregulation (zum Beispiel durch Checklisten zur Klausurvorbereitung)
- kognitive Aktivierung (zum Beispiel durch angepasste Anforderungen an verschiedene Lernvoraussetzungen) [14]
Im Folgenden werden verschiedene Beispiele für differenzierende aufgabenbezogene Methoden vorgestellt.
Siehe auch: Binnendifferenzierung
Optionale Teilaufgaben

Zusatzaufgaben werden als differenzierende und optionale Aufgaben angeboten. Die Lernenden entscheiden individuell und je nach Leistungsstand, ob sie die Bearbeitung dieser Aufgaben für den eigenen Lernprozess als sinnvoll erachten.
Die Bearbeitung dieser Aufgaben sollte eine angemessene Bewertung und Wertschätzung zugesprochen werden, da diese sonst schnell als Beschäftigungsvorwand von den Lernenden interpretiert werden.
Blütenaufgaben
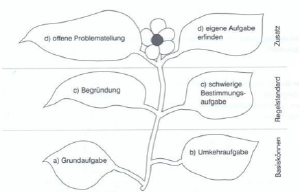
Beide Grundaufgaben sind zu bearbeiten. Beim Aufstieg der Blüte bestehen Wahlmöglichkeiten. [16]
Blütenaufgaben sind anforderungsgestufte Aufgaben, bestehend aus mehreren Teilaufgaben mit zunehmendem Anspruchsniveau zum selben Themenkontext. Blütenaufgaben beginnen mit einer geschlossenen Einstiegsaufgabe, die den Schülerinnen und Schüler zugänglich ist. Es folgen weitere offene Teilaufgaben mit gestuften Anforderungen. Dieser Aufgabentyp ermöglicht, dass mit einer einzigen Aufgabe Grundanforderungen gestellt und weiterführende Anforderungen geöffnet werden können. [17] [18]
Aufgabensets
Ein Aufgabenset beinhaltet circa zehn schwierigkeitsgestufte Aufgaben zu einem Thema aus dem (inner-)mathematischen Kontext, welche gezielt für eine einzelne Übungsphase zusammengestellt werden. Dabei bearbeitet die einzelne Schülerin bzw. der einzelne Schüler nicht alle zehn Aufgaben, sondern nur eine bestimmte Anzahl der vorgegebenen Aufgaben. Die ersten Aufgaben bewegen sich im Anforderungsbereich I und beinhalten hauptsächlich Grundaufgaben und Aufgabenumkehrungen. Die nächsten Aufgaben sind dem Anforderungsbereich II zuzuordnen und beinhalten Anwendungen oder erste Verallgmeinerungen. Die letzten Aufgaben sind dem dritten Anforderungsbereich zuzuordnen. Hierbei werden vertiefende Transferaufgaben behandelt. Die Zusammenstellung der Inhalte und die Wahlmöglichkeiten gewährleisten, dass die Lernenden entsprechend ihres Festigungsbedarfs und ihres Leistungsvermögens angemessen gefördert und gefordert werden. [19]
Prozessorientierte Aufgaben
Prozessorientierte Aufgaben konzentrieren sich auf die anzuwendenden Prozesse des Problemlösens oder Modellierens. Die Kenntnisse von mathematischen Inhalten rückt hierbei eher in den Hintergrund.
Ein Beispiel prozessorientierter Aufgaben im Mathematikunterricht sind Modellierungsaufgaben. Die Kompetenz des Modellierens beinhaltet „realitätsbezogene Situationen durch den Einsatz mathematischer Mittel zu verstehen, zu strukturieren und das der Situation zugrunde liegende Problem einer Lösung zuzuführen sowie Mathematik in der Realität zu erkennen und zu beurteilen.“ [21]
Phasen und Ziele von Modellierungsaufgaben
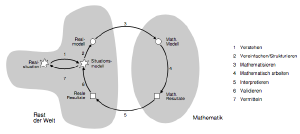
Die verschiedenen Phasen eines Modellierungsprozesses sind in der seitlich aufgeführten Grafik visualisiert. Die von den Schülerinnen und Schülern zu vollzuiehenden Teilschritte sind folgende:
- Verstehen: Aufgabenstellung verstehen und Situationsmodell bilden
- Vereinfachen/ Strukturieren: Durch Treffen geeigneter Annahmen wird das Situationsmodell strukturiert, idealisiert und präzisiert sowie ein Realmodell konstruiert
- Mathematisieren: Das Realmodell wird in ein mathematisches Modell transformiert
- Mathematisch arbeiten: Ein ausgewähltes mathematisches Verfahren wird angewendet und ein mathematisches Resultat hergeleitet
- Interpretieren: Das mathematische Resultat wird interpretiert und in ein reales Resultat transformiert
- Validieren: Dieses reale Resultat wird unter der Gegebenheiten der Situation überprüft
- Vermitteln: Der Lösungsprozess wird nachvollziehbar dokumentiert [22]
Durch den Einsatz und die Anwendung von Modellierungsaufgaben im Unterricht werden inhaltsorientierte (Erschließung der realen Welt mit mathematischen Mitteln), prozessbezogene (Ausbildung mathematischer Problemlösefähigkeiten, wie zum Beispiel heuristischer Strategien) und allgemeine Ziele (kulturbezogene Vermittlung von der Verwendung der Mathematik in der realen Welt, als zentraler Aspekt für die Entwicklung der Mathematik als Wissenschaft, dazu zählt auch die kritische Reflexion mathematischer Modelle in der Gesellschaft) verfolgt. [23]
Diagnoseaufgaben
Diagnoseaufgaben sind ein mögliches Werkzeug, Erkenntnisse über den aktuellen Wissensstand und vorhandene mathematische Problemlösefähigkeiten der Lernenden in Erfahrung zu bringen. Sie können außerdem Hinweise darauf geben, worin genau Kenntnisdefizite beim Verständnis mathematischer Sachverhalte vorhanden sind. Dies ist insbesondere für die Bereitstellung individueller Förderangebote von großer Bedeutung.
Diagnoseaufgaben sollten bestimmte Bedingungen erfüllen:
- Sie sollten eine erkennbare Relation zwischen entstehenden Schülerlösungen und systematischen Fehlerstrategien herstellen können. Dies dient der Vergleichbarkeit der entstehenden Ergebnisse und somit der qualitativen Einschätzung dieser.
- Um eine detaillierte Fehlerstrategieanalyse zu ermöglichen sollten die Lösungswege der Schülerinnen und Schüler begründet dargelegt werden.
- Um bei der Anwendung von Diagnoseaufgaben die Erhebung des Umgangs mit Zeit- und Leistungsdruck auszuschließen, sollten Diagnoseaufgaben von Leistungsbewertungen entkoppelt sein.
- Leistungsstanddiagnosen sollten langfristig, hinsichtlich bestimmter Variablen, angelegt sein, um eine möglichst vielsietige und fundiert Diagnose zu gewährleisten.
- Für den Vergleich des Lernendenselbstkozenpts mit dem tatsächlichen Lernstand sollte eine Selbsteinschätzung oder eine Reflexion in der Diagnose des Leistungsstands implementiert sein. [24]
Einzelnachweise
- ↑ Bruder, R.(2000): Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung - Wege zu einem anspruchsvollen Mathematikunterricht für alle. In: Flade & Herget (Hrsg.): Mathematik lehren und lernen nach TIMSS. Anregungen für die Sekundarstufen. Berlin: Volk und Wissen. ISBN 3060023654.
- ↑ Leuders, T. (2018): Mathematik Didaktik. Praxishandbuch für die Sekundarstufe I und II. Berlin: Cornselsen Verlag Scripor GmbH&Co. KG. S. 300ff. ISBN 3589216956
- ↑ Karikatur von Michael Hüter aufgerufen unter: https://docplayer.org/docs-images/66/55548085/images/10-1.jpg Stand: 01.09.2020
- ↑ Bruder, R. (2006): Modul 1: Weiterentwicklung der Aufgabenkultur im Mathematikunterricht. Aufgerufen auf: http://www.sinus-transfer.de/fileadmin/MaterialienBT/Bruder_Modul1.pdf Stand: 02.09.2020
- ↑ PISA 2003, Ergebnisse des zweiten Internationalen Vergleichs, Zusammenfassung unter: http://archiv.ipn.uni-kiel.de/PISA/PISA2003_E_Zusammenfassung.pdf, S.18
- ↑ vgl. Neubrand, J. (2002): Eine Klassifikation mathematischer Aufgaben zur Analyse von Unterrichtssituationen. Selbsttätiges Arbeiten in Schülerarbeitsphasen in den Stunden der TIMSS-Video-Studie. Hildesheim/Berlin: Franzbecker. ISBN 3881203443
- ↑ Pekrun, R.; Götz, T.; vom Hofe, R.; Blum, W.; Jullien, S.; Zirngibl, A.; Kleine, M.; Wartha, S.; Jordan, A. (2004): Emotionen und Leistung im Fach Mathematik: Ziele und erste Befunde aus dem „Projekt zur Analyse der Leistungsentwicklung in Mathematik“ (PALMA), Münster: Waxmann, S.359, ISBN 3830913990
- ↑ Bruder, R. (2006): Modul 1: Weiterentwicklung der Aufgabenkultur im Mathematikunterricht. Aufgerufen auf: http://www.sinus-transfer.de/fileadmin/MaterialienBT/Bruder_Modul1.pdf Stand: 02.09.2020
- ↑ Bruder, R.(2000): Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung - Wege zu einem anspruchsvollen Mathematikunterricht für alle. In: Flade & Herget (Hrsg.): Mathematik lehren und lernen nach TIMSS. Anregungen für die Sekundarstufen. Berlin: Volk und Wissen. ISBN 3060023654. Aufgerufen auf: https://slideplayer.org/slide/11869083/ Stand: 02.09.2020
- ↑ Bruder, R.(2000): Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung - Wege zu einem anspruchsvollen Mathematikunterricht für alle. In: Flade & Herget (Hrsg.): Mathematik lehren und lernen nach TIMSs. Anregungen für die Sekundarstufen. Berlin: Volk und Wissen. ISBN 3060023654
- ↑ Bruder, R.(2000): Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung - Wege zu einem anspruchsvollen Mathematikunterricht für alle. In: Flade & Herget (Hrsg.): Mathematik lehren und lernen nach TIMSS. Anregungen für die Sekundarstufen. Berlin: Volk und Wissen. ISBN 3060023654
- ↑ Bruder, R.(2000): Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung - Wege zu einem anspruchsvollen Mathematikunterricht für alle. In: Flade & Herget (Hrsg.): Mathematik lehren und lernen nach TIMSS. Anregungen für die Sekundarstufen. Berlin: Volk und Wissen. ISBN 3060023654
- ↑ Bruder, R.(2000): Eine akzentuierte Aufgabenauswahl und Vermitteln heuristischer Erfahrung - Wege zu einem anspruchsvollen Mathematikunterricht für alle. In: Flade & Herget (Hrsg.): Mathematik lehren und lernen nach TIMSS. Anregungen für die Sekundarstufen. Berlin: Volk und Wissen. ISBN 3060023654
- ↑ Roder, U. & Bruder, R. (2015): MAKOS – Ein Projekt zur Umsetzung der Abiturstandards Mathematik in Hessen. In G. Kaiser & H.-W. Henn (Hrsg.), Werner Blum und seine Beiträge zum Modellieren. Festschrift zum 70. Geburtstag. Wiesbaden: Springer Spektrum Verlag. S. 284 ISBN 9783658095314
- ↑ Aufgerufen unter: https://unterrichten.zum.de/images/8/8a/Förderaufgabe.png Stand: 01.09.2020
- ↑ Storz, R. (2014): Mathematik differenziert und individualisiert unterrichten. Hallbergmoos: Aulis Verlag. S. 143 ISBN 9783761429266
- ↑ Zeitler, H. (2013): In der Vielfalt liegt die Stärke - Handreichung zur Individualisierung des Lernens für die gesellschaftswissenschaftlichen Fächer. Berlin: Ruksaldruck GmbH, S.17f ISBN 9783944541020
- ↑ Storz, R. (2014): Mathematik differenziert und individualisiert unterrichten. Hallbergmoos: Aulis Verlag. S. 142ff ISBN 9783761429266
- ↑ Roder, U. & Bruder, R. (2015): MAKOS – Ein Projekt zur Umsetzung der Abiturstandards Mathematik in Hessen. In G. Kaiser & H.-W. Henn (Hrsg.), Werner Blum und seine Beiträge zum Modellieren. Festschrift zum 70. Geburtstag. Wiesbaden: Springer Spektrum Verlag. S. 290. ISBN 9783658095314
- ↑ Blum, W. & Leiß, D. (2005): Modellieren im Unterricht mit der “Tanken”-Aufgabe, In: Mathematik lehren, H. 128, Feb. 2005, S. 19. Hannover: Friedrich Verlag
- ↑ Leiß, D., & Blum, W. (2006): Beschreibung zentraler mathematischer Kompetenzen. In: W. Blum, C. Drüke-Noe, R. Hartung, & O. Köller (Hrsg.): Die Bildungsstandards Mathematik (S. 33–50). Berlin: Cornelsen Scriptor. S. 41f
- ↑ Achmetli, K., Krug, A., Schukajlow,S. (2015): Multiple Lösungsmöglichkeiten und ihre Nutzung beim mathematischen Modellieren. In: G. Kaiser & H.-W. Henn (Hrsg.), Werner Blum und seine Beiträge zum Modellieren. Festschrift zum 70. Geburtstag. Wiesbaden: Springer Spektrum Verlag. S. 26 ISBN 9783658095314
- ↑ Ferri, R., Greefrath, G., Kaiser, G. (2013): Mathematisches Modellieren für Schule und Hochschule. Wiesbaden: Springer Spektrum. S. 20
- ↑ Leuders, T. (2018): Mathematik Didaktik. Praxishandbuch für die Sekundarstufe I und II. Berlin: Cornselsen Verlag Scripor GmbH&Co. KG. S. 302f. ISBN 3589216956