Aufgabentypen

Zur Etablierung einer lernförderlichen Aufgabenkultur sollten verschiedene Aufgabentypen angewendet werden. Man kann hierbei zwischen differenzierenden, prozessorientierten und Diagnoseaufgaben unterscheiden.

Karikatur von Michael Hüter

Relevanz

Die Relevanz zur Weiterentwicklung der Aufgabenkultur lässt sich in empirischen Untersuchungen der letzten Jahre wiederfinden. Gemeinsame Ursachen für auftretende Phänomene ist auf eine unzureichend ausgeprägte Aufgabenkultur im Mathematikunterricht deutscher Schulen zurückzuführen.
Exemplarische Beispiele werden im Folgenden genannt:

• Lernende aus Deutschland weisen in der PISA-Studie 2003 deutlich höhere Werte im Bereich der Problemlösefähigkeiten im Vergleich zu der mathematischen Kompetenz auf. Diesen Befund weisen nur sehr wenige Staaten im internationalen Vergleich auf. Dieser Befund kann dahingehend interpretiert werden, dass das kognitive Potenzial deutscher Schülerinnen und Schüler weniger erfolgreich in mathematische Kompetenz umgesetzt wird.
• Die TIMSS-Studie weist auf, dass im Mathematikunterricht an deutschen Schule komplexe Aufgaben am wenigsten gestellt werden, im Vergleich zu den USA und Japan.
• Inhaltliches mathematisches Denken von Lernenden der Klassenstufen 5 und 6 werden durch die Anwendung erlernter kalkülhafter Regeln ersetzt.

Die genannten empirischen Phänomene weisen keineswegs eine geringere Leistungsfähigkeit deutscher Schülerinnen und Schüler im internationalen Vergleich auf. Es besteht allerdings grundlegender Bedarf diese Leistungsfähigkeit im Mathematikunterricht abzurufen. Dabei sollte unter anderem die Entwicklung eine lernförderlichen Aufgabenkultur eine zentrale Rolle spielen.
Im Folgenden werden Möglichkeiten zur Umsetzung dieses Ziels dargestellt.

Aufgabentypen nach Bruder

Aufgabentypen nach Bruder (2000)

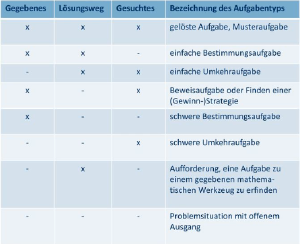
Diese Aufgabentypen bilden wesentliche Lerntätigkeiten ab, ermöglichen Vernetzung, bieten individuelle Freiräume und erfordern methodische Variabilität des Unterrichts. Aktivieren kognitiv.

Differenzierende Aufgaben

Differenzierende Aufgaben berücksichtigen in besonderem Maße unterschiedliche Niveaustufen der Lernenden, sodass Aufgaben je nach individuellem Vorwissen und Leistungsstand bearbeitet werden können. Eckpfeiler differenziernden Unterrichts sind:

• Sicherung des Ausgangsniveaus (zum Beispiel durch vermischte Kopfübungen)
• Ziel- und Inhaltstransparenz (zum Beispiel durch Lernprotokolle)
• Förderung der Selbstregulation (zum Beispiel durch Checklisten zur Klausurvorbereitung)
• kognitive Aktivierung (zum Beispiel durch angepasste Anforderungen an verschiedene Lernvoraussetzungen)

Im Folgenden werden verschieden Beispiele für differenzierende aufgabenbezogene Methoden vorgestellt. Grundlegende Ansätze differenzierenden Unterrichts erhalten Sie auf der Seite: Binnendifferenzierung

Optionale Teilaufgaben

Auf der Seite ZUM-Unterrichten werden optionale Zusatz- und Förderaufgaben mit diesem Zeichen gekennzeichnet.

Zusatzaufgaben werden als differenzierende und optionale Aufgaben angeboten. Die Lernenden entscheiden individuell und je nach Leistungsstand, ob sie die Bearbeitung dieser Aufgaben für den eigenen Lernprozess als sinnvoll erachten.
Die Bearbeitung dieser Aufgaben sollte eine angemessene Bewertung und Wertschätzung zugesprochen werden, da diese sonst schnell als Beschäftigungsvorwand von den Lernenden interpretiert werden.

Blütenaufgaben

Visualisierung des typischen Aufbaus einer Blütenaufgabe.
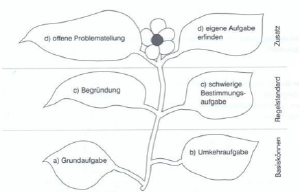
Beide Grundaufgaben sind zu bearbeiten. Beim Aufstieg der Blüte bestehen Wahlmöglichkeiten.

Blütenaufgaben sind Anforderungsgestufte Aufgaben, bestehend aus mehreren Teilaufgaben mit zunehmendem Anspruchsniveau zum selben Themenkontext. Blütenaufgaben beginnen mit einer geschlossenen Einstiegsaufgabe, die den Schülerinnen und Schüler zugänglich ist. Es folgen weitere offene Teilaufgaben mit gestuften Anforderungen. Dieser Aufgabentyp ermöglicht, dass mit einer einzigen Aufgabe Grundanforderungen gestellt und weiterführende Anforderungen geöffnet werden können.

Aufgabensets

Ein Aufgabenset beinhaltet circa zehn schwierigkeitsgestufte Aufgaben zu einem Thema aus dem (inner-)mathematischen Kontext, die gezielt für eine einzelne Übungsphase zusammengestellt werden. Dabei bearbeiten die einzelne Schülerin, der einzelne Schüler nicht alle zehn Aufgaben, sondern nur eine bestimmt vorgegebene Anzahl an Aufgaben. Die ersten Aufgaben bewegen sich im Anforderungsbereich I und beinhalten hauptsächlich Grundaufgaben und Aufgabenumkehrungen. Die nächsten Aufgaben sind dem Anforderungsbereich II zuzuordnen und beinhalten Anwendungen oder erste Verallgmeinerungen. Die letzten Aufgaben sind dem dritten Anforderungsbereich zuzuordnen. Hierbei werden vertiefende Transferaufgaben behandelt. Die Zusammenstellung der Inhalte und die Wahlmöglichkeiten gewährleisten, dass die Lernenden entsprechend ihres Festigungsbedarfs und ihres Leistungsvermögens angemessen gefördert und gefordert werden.

Prozessorientierte Aufgaben

Visualisierung des Modellierungskreislaufs nach Blum & Leiß (2005).

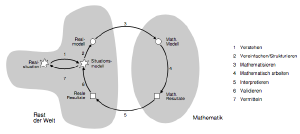
Prozessorientierte Aufgaben konzentrieren sich auf die anzuwendenden Prozesse des Problemlösens oder Modellierens. Die Kenntnisse von mathematischen Inhalten rückt hierbei eher in den Hintergrund.

Diagnoseaufgaben

Diagnoseaufgaben sind ein mögliches Werkzeug Erkenntnisse über den aktuellen Wissensstand und vorhandene mathematische Problemlösefähigkeiten der Lernenden in Erfahrung zu bringen. Sie können außerdem Hinweise darauf geben worin genau Kenntnisdefizite beim Verständnis mathematischer Sachverhalte vorhanden sind. Dies ist insbesondere für die Bereitstellung individueller Förderangebote von großer Bedeutung.
Diagnoseaufgaben sollten bestimmte Bedingungen erfüllen:

• Relation zwischen entstehenden Schülerlösungen und systematischen Fehlerstrategien
• Lösungswege sollen begründet und dargelegt werden
• von Leistungsbewertung entkoppelt
• langfristig angelegte, hinsichtlich bestimmter Variablen, Diagnose
• Implementierung einer Selbsteinschätzung oder Reflexion