Schrankenkriterium: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (10 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 30: | Zeile 30: | ||
====Raumschranke==== | ====Raumschranke==== | ||
*Vernetzung verteilter Lernobjekte-/orte | *Vernetzung verteilter Lernobjekte-/orte | ||
*Bereitstellung von Simulationen | *Bereitstellung von Simulationen | ||
| Zeile 36: | Zeile 35: | ||
*Umsetzung von Augmented Reality | *Umsetzung von Augmented Reality | ||
*Umsetzung von Virtual Reality | *Umsetzung von Virtual Reality | ||
===Graduierung=== | ===Graduierung=== | ||
| Zeile 53: | Zeile 44: | ||
==Weiterführende Hinweise== | ==Weiterführende Hinweise== | ||
*Der Begriff des Mehrwerts muss stets kritisch aufgefasst werden. Er soll nicht den Anschein erwecken, Digitales setze die Lernziele aus traditionellem Unterricht effektiver und effizienter um. Stattdessen muss immer die Entwicklung der Zielvorstellung mit der Wahl des (digitalen) Mediums und der Methode einher gehen. Die Frage nach dem Mehrwert, und damit das Kriterium, ist auch beantwortet, bzw. erfüllt, wenn ein Unentschieden zwischen digitaler und analoger Variante existiert. Im selben Zuge sollte auch die Wahl traditioneller Medien stets einen Mehrwerttest unterzogen werden. Für eine ausführliche Auseinandersetzung Vgl. [https://routenplaner-digitale-bildung.de/ Routenplaner #digitaleBildung], „Wider den Mehrwert! Argumente gegen einen überflüssigen Begriff“ von Axel Krommer | |||
*Die Normen - und Werteschranke gehört eigentlich mit zum Schrankenkriterium. Sie wird hier nicht weiter gewichtet, da sie durch die Kriterien [[Barrierefreiheit in der individuellen Nutzung]] und [[nachgehende Differenzierung]] abgedeckt ist. | *Die Normen - und Werteschranke gehört eigentlich mit zum Schrankenkriterium. Sie wird hier nicht weiter gewichtet, da sie durch die Kriterien [[Barrierefreiheit in der individuellen Nutzung]] und [[nachgehende Differenzierung]] abgedeckt ist. | ||
*Die Analog-Digital-Schranke wird hier nicht weiter gewichtet, da sie durch das Kriterium [[Mehrperspektivität]] abgedeckt ist. | *Die Analog-Digital-Schranke wird hier nicht weiter gewichtet, da sie durch das Kriterium [[Mehrperspektivität]] abgedeckt ist. | ||
| Zeile 61: | Zeile 53: | ||
**Überwindung von Risikoschranken, durch Virtualisierung entsprechender Einrichtungen und Gegenstände | **Überwindung von Risikoschranken, durch Virtualisierung entsprechender Einrichtungen und Gegenstände | ||
*Auch wurde das Arbeiten mit realen Daten erst möglich durch den Einsatz des Rechners. So kann zum Beispiel durch den Rechnereinsatz im Mathematikunterricht die Beziehung zwischen Mathematik und dem Rest der Welt, durch Realbezüge, berücksichtigt werden. (siehe [[Fachliche Zielsetzung#Weiterführende Hinweise|Computational offloading]]) <ref> Langlotz, H. / Stachniss-Carp, S. / Weller, H.: Mathematikunterricht mit digitalen Werkzeugen – Eine persönliche Bilanz von 25 Jahren Einsatz im Unterricht. In (Büchter, A.; Glade, M.; Herold-Blasius, R. Hrsg.): Vielfältige Zugänge zum Mathematikunterricht. Konzepte und Beispiele aus Forschung und Praxis, 2019, S. 210 f., ISBN 3658242922.</ref> | *Auch wurde das Arbeiten mit realen Daten erst möglich durch den Einsatz des Rechners. So kann zum Beispiel durch den Rechnereinsatz im Mathematikunterricht die Beziehung zwischen Mathematik und dem Rest der Welt, durch Realbezüge, berücksichtigt werden. (siehe [[Fachliche Zielsetzung#Weiterführende Hinweise|Computational offloading]]) <ref> Langlotz, H. / Stachniss-Carp, S. / Weller, H.: Mathematikunterricht mit digitalen Werkzeugen – Eine persönliche Bilanz von 25 Jahren Einsatz im Unterricht. In (Büchter, A.; Glade, M.; Herold-Blasius, R. Hrsg.): Vielfältige Zugänge zum Mathematikunterricht. Konzepte und Beispiele aus Forschung und Praxis, 2019, S. 210 f., ISBN 3658242922.</ref> | ||
[[Datei:Schrankenkrit_geoGebraAR.jpg|thumb|Würfelnetz in Augmented Reality]] | |||
*Somit bietet die Technologie auch die Möglichkeit neue Problemlösungsumgebungen zu erschaffen. <ref> Thurm, D.: Teacher Beliefs and Practice When Teaching with Technology: A Latent Profile Analysis. In (Ball, L., Drijvers, P. et al. Hrsg.): Uses of Technology in Primary and Secondary Mathematics Education: Tools, Topics and Trends. Springer International Publishing: Cham, Switzerland., 2018, S. 145 ISBN 9783319765747</ref> | *Somit bietet die Technologie auch die Möglichkeit neue Problemlösungsumgebungen zu erschaffen. <ref> Thurm, D.: Teacher Beliefs and Practice When Teaching with Technology: A Latent Profile Analysis. In (Ball, L., Drijvers, P. et al. Hrsg.): Uses of Technology in Primary and Secondary Mathematics Education: Tools, Topics and Trends. Springer International Publishing: Cham, Switzerland., 2018, S. 145 ISBN 9783319765747</ref> | ||
| Zeile 67: | Zeile 60: | ||
*Wie oben bereits genannt, können in der Physik und Chemie Experimente, die zu gefährlich für die Schule sind, durch Virtual Reality umgesetzt und gezeigt werden. Aber auch Experimente, die über einen langen oder kurzen Zeitraum ablaufen, können so genauer gezeigt werden. Zum Beispiel in der Physik die Verformung von Körpern beim Zusammenstoß. | *Wie oben bereits genannt, können in der Physik und Chemie Experimente, die zu gefährlich für die Schule sind, durch Virtual Reality umgesetzt und gezeigt werden. Aber auch Experimente, die über einen langen oder kurzen Zeitraum ablaufen, können so genauer gezeigt werden. Zum Beispiel in der Physik die Verformung von Körpern beim Zusammenstoß. | ||
*Aber auch Mikro- und Makrowelten können mit Hilfe Virtual Reality oder Augmented Reality dargestellt werden. Zum Beispiel könnten hier Zellen oder auch das Sonnensystem dargestellt werden. | *Aber auch Mikro- und Makrowelten können mit Hilfe Virtual Reality oder Augmented Reality dargestellt werden. Zum Beispiel könnten hier Zellen oder auch das Sonnensystem dargestellt werden. | ||
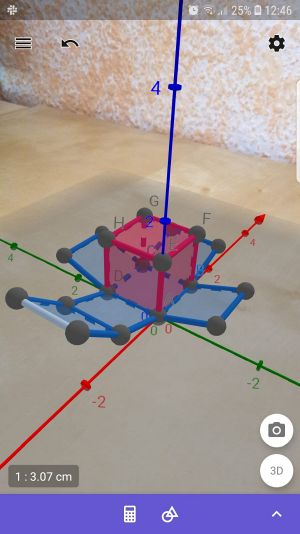
Als Beispiel, wie Augmented Reality im Mathematikunterricht genutzt werden kann, zeigt GeoGebra. Diese Software zur Veranschaulichung von mathematischen Problemen wird bereits meistens im Mathematikunterricht eingesetzt. Doch gibt es für Handys und Tabletts (für [https://play.google.com/store/apps/details?id=org.geogebra.android.g3d&hl=de Android] und [https://apps.apple.com/de/app/geogebra-augmented-reality/id1276964610 IOS]) eine App, mit der sich die Schülerinnen und Schüler ihre Funktionen und dreidimensionalen Körper selbstständig anschauen und mit der Anwendung experimentieren können. | |||
[[Datei:Schrankenkrit_MessenAR.jpg|thumb|Messen der Länge des Brettchens mit Hilfe der App]] | |||
Ein weiteres Tool könnte das Vermessen von Gegenständen mit Hilfe des Handys sein. So können zum Beispiel die geschätzte Höhe oder Länge eines Gebäudes oder Baumes mit Hilfe von Augmented Reality überprüft werden. Dabei sollte auf die Kalibrierung geachtet werden. | |||
Eine Einsatzmöglichkeit könnte sein, dass der Lehrer im Rahmen einer Projektwoche zum Lernbereich 3 Rechtwinklige Dreiecke <ref>Sächsisches Staatsministerium für Kultus - Freistaat Sachsen: Lehrplan Gymnasium Mathematik. | |||
2004/2009/2011/2013/2019. | |||
https://www.schule.sachsen.de/lpdb/web/downloads/2426_lp_gy_mathematik_2019_final.pdf?v2, Stand: | |||
21.04.2020. S.25 </ref> in der 9. Klasse die Höhe eines Gebäudes in der Umgebung bestimmt. Dazu können die Schülerinnen und Schüler mit Hilfe der genannten App den Abstand vom Haus zu einem anderen Punkt bestimmen. Im Anschluss kann zum Beispiel mit Hilfe der [https://play.google.com/store/apps/details?id=de.rwth_aachen.phyphox&hl=de phyphox-App], der Winkel bestimmt werden unter dem man die Spitze des Daches sehen kann. Somit kann die Höhe des Hauses errechnet werden. | |||
== Einzelnachweise == | == Einzelnachweise == | ||
Aktuelle Version vom 18. Februar 2021, 09:48 Uhr
| Steckbrief | |
|---|---|
| Name | Schrankenkriterium |
| Dimension | didaktisch |
| Notwendigkeit für das Szenario | obligatorisch |
| Messbarkeit | absolut |
Das Schrankenkriterium umfasst die Nutzung digitaler Medien, um unterschiedliche Schranken durch E-Learning im Unterrichtsprozess zu überwinden.
Dabei liegt der Fokus auf dem didaktischen Mehrwert:
- Entstehen durch die Nutzung des digitalen Mediums technische, organisatorische, kommunikative oder informationelle Vorteile und expandieren dadurch die Lernchancen der Lernenden?[1]
Der technische Komfort, die Unterstützung und Erleichterung der Kommunikation oder der Zugang zu Informationen sind zwar Vorteile von E-Learning, sie beschreiben allerdings nur eine Ablösung der analogen Varianten. Ein didaktischer Mehrwert geht somit immer mit der Expansion der Lernchancen einher. Die Normen- und Werteschranke sowie die Analog-Digital-Schranke sind in den Kriterien Barrierefreiheit in der individuellen Nutzung, nachgehende Differenzierung und Mehrperspektivität abgedeckt und werden hier nicht weiter betrachtet.
Kriterium
Die effektive und effiziente Nutzung des digitalen Mediums ermöglicht das Überwinden der Zeit - und Raumschranke des E-Learning, expandiert die Lernchancen und sichert einen Mehrwert gegenüber analogen Alternativen.
Beschreibung
Zu prüfende Merkmale
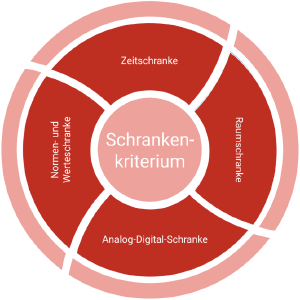
Bei der Prüfung der Schranken muss stets die Frage nach dem didaktischen Mehrwert gestellt werden: Entstehen durch die Nutzung des digitalen Mediums technische, organisatorische, kommunikative oder informationelle Vorteile und expandieren dadurch die Lernchancen der Lernenden? [2]
Zeitschranke
- Vernetzung von synchron/asynchron Lernphasen
- Expansion der Lernzeit
- Virtualisierung der Zeit (Zeitraffer/Zeitlupe/Start/Stopp)
- Nutzung einer außerschulischen Kommunikation
- digitale Unterrichtskonzepte (Blended Learning, Inverted Classroom)
Raumschranke
- Vernetzung verteilter Lernobjekte-/orte
- Bereitstellung von Simulationen
- Zugang zu Mikro - und Makrowelten [3]
- Umsetzung von Augmented Reality
- Umsetzung von Virtual Reality
Graduierung
| Beschreibung | |
| Stufe 0 | Das digitale Medium überwindet keine der beiden Schranken. |
| Stufe 1 | Das digitale Medium überwindet mindestens die Zeitschranke oder die Raumschranke. |
| Stufe 2 | Das digitale Medium überwindet sowohl die Zeitschranke als auch die Raumschranke. |
Weiterführende Hinweise
- Der Begriff des Mehrwerts muss stets kritisch aufgefasst werden. Er soll nicht den Anschein erwecken, Digitales setze die Lernziele aus traditionellem Unterricht effektiver und effizienter um. Stattdessen muss immer die Entwicklung der Zielvorstellung mit der Wahl des (digitalen) Mediums und der Methode einher gehen. Die Frage nach dem Mehrwert, und damit das Kriterium, ist auch beantwortet, bzw. erfüllt, wenn ein Unentschieden zwischen digitaler und analoger Variante existiert. Im selben Zuge sollte auch die Wahl traditioneller Medien stets einen Mehrwerttest unterzogen werden. Für eine ausführliche Auseinandersetzung Vgl. Routenplaner #digitaleBildung, „Wider den Mehrwert! Argumente gegen einen überflüssigen Begriff“ von Axel Krommer
- Die Normen - und Werteschranke gehört eigentlich mit zum Schrankenkriterium. Sie wird hier nicht weiter gewichtet, da sie durch die Kriterien Barrierefreiheit in der individuellen Nutzung und nachgehende Differenzierung abgedeckt ist.
- Die Analog-Digital-Schranke wird hier nicht weiter gewichtet, da sie durch das Kriterium Mehrperspektivität abgedeckt ist.
- Unter der Zeitschranke versteht man, dass die Lernzeit individualisiert wird.
- Beispiele für die Raumschranke:
- globaler Zugang zu raren Ressourcen
- Überwindung natürliche Zugangsschranken durch "verlangsamen der Zeit"
- Überwindung von Risikoschranken, durch Virtualisierung entsprechender Einrichtungen und Gegenstände
- Auch wurde das Arbeiten mit realen Daten erst möglich durch den Einsatz des Rechners. So kann zum Beispiel durch den Rechnereinsatz im Mathematikunterricht die Beziehung zwischen Mathematik und dem Rest der Welt, durch Realbezüge, berücksichtigt werden. (siehe Computational offloading) [4]
- Somit bietet die Technologie auch die Möglichkeit neue Problemlösungsumgebungen zu erschaffen. [5]
Praxisbeispiel
Folgende Ideen überwinden bspw. die Raum- und Zeitschranke:
- Wie oben bereits genannt, können in der Physik und Chemie Experimente, die zu gefährlich für die Schule sind, durch Virtual Reality umgesetzt und gezeigt werden. Aber auch Experimente, die über einen langen oder kurzen Zeitraum ablaufen, können so genauer gezeigt werden. Zum Beispiel in der Physik die Verformung von Körpern beim Zusammenstoß.
- Aber auch Mikro- und Makrowelten können mit Hilfe Virtual Reality oder Augmented Reality dargestellt werden. Zum Beispiel könnten hier Zellen oder auch das Sonnensystem dargestellt werden.
Als Beispiel, wie Augmented Reality im Mathematikunterricht genutzt werden kann, zeigt GeoGebra. Diese Software zur Veranschaulichung von mathematischen Problemen wird bereits meistens im Mathematikunterricht eingesetzt. Doch gibt es für Handys und Tabletts (für Android und IOS) eine App, mit der sich die Schülerinnen und Schüler ihre Funktionen und dreidimensionalen Körper selbstständig anschauen und mit der Anwendung experimentieren können.

Ein weiteres Tool könnte das Vermessen von Gegenständen mit Hilfe des Handys sein. So können zum Beispiel die geschätzte Höhe oder Länge eines Gebäudes oder Baumes mit Hilfe von Augmented Reality überprüft werden. Dabei sollte auf die Kalibrierung geachtet werden. Eine Einsatzmöglichkeit könnte sein, dass der Lehrer im Rahmen einer Projektwoche zum Lernbereich 3 Rechtwinklige Dreiecke [6] in der 9. Klasse die Höhe eines Gebäudes in der Umgebung bestimmt. Dazu können die Schülerinnen und Schüler mit Hilfe der genannten App den Abstand vom Haus zu einem anderen Punkt bestimmen. Im Anschluss kann zum Beispiel mit Hilfe der phyphox-App, der Winkel bestimmt werden unter dem man die Spitze des Daches sehen kann. Somit kann die Höhe des Hauses errechnet werden.
Einzelnachweise
- ↑ Schulmeister, R.: eLearning: Einsichten und Aussichten. Oldenbourg, München, 2006, S. 209, ISBN 9783486580037.
- ↑ Schulmeister, R.: eLearning: Einsichten und Aussichten. Oldenbourg, München, 2006, S. 209, ISBN 9783486580037.
- ↑ Krauthausen, G.: Digitale Medien im Mathematikunterricht der Grundschule. Spektrum Akademischer Verlag, Berlin, 2012, S. 88 f., ISBN 9783827422767.
- ↑ Langlotz, H. / Stachniss-Carp, S. / Weller, H.: Mathematikunterricht mit digitalen Werkzeugen – Eine persönliche Bilanz von 25 Jahren Einsatz im Unterricht. In (Büchter, A.; Glade, M.; Herold-Blasius, R. Hrsg.): Vielfältige Zugänge zum Mathematikunterricht. Konzepte und Beispiele aus Forschung und Praxis, 2019, S. 210 f., ISBN 3658242922.
- ↑ Thurm, D.: Teacher Beliefs and Practice When Teaching with Technology: A Latent Profile Analysis. In (Ball, L., Drijvers, P. et al. Hrsg.): Uses of Technology in Primary and Secondary Mathematics Education: Tools, Topics and Trends. Springer International Publishing: Cham, Switzerland., 2018, S. 145 ISBN 9783319765747
- ↑ Sächsisches Staatsministerium für Kultus - Freistaat Sachsen: Lehrplan Gymnasium Mathematik. 2004/2009/2011/2013/2019. https://www.schule.sachsen.de/lpdb/web/downloads/2426_lp_gy_mathematik_2019_final.pdf?v2, Stand: 21.04.2020. S.25