Darstellungswechsel: Unterschied zwischen den Versionen

Aus digiteach
Zur Navigation springen Zur Suche springen
Zeile 23: Zeile 23:
#'''Zu prüfende Merkmale hinsichtlich der Verknüpfung sind:'''  
#'''Zu prüfende Merkmale hinsichtlich der Verknüpfung sind:'''  
#*Enaktive, ikonische und symbolische Darstellungen eines fachlichen Inhalts können interaktiv verknüpft werden (bspw. mit Multi-Touch-Funktion <ref>Walter, D.: Nutzungsweisen bei der Verwendung von Tablet-Apps. Dissertation, 2018, S. 56-62, ISBN 3658190671.</ref><ref>Drijvers, P.: Head in the clouds, feet in the ground – A realistic view on using digital tools in mathematics education. In (Büchter, A.; Glade, M.; Herold-Blasius, R. Hrsg.): Vielfältige Zugänge zum Mathematikunterricht. Konzepte und Beispiele aus Forschung und Praxis, 2019, S. 173, ISBN 3658242922.</ref>). Dabei werden die Auswirkungen der Änderungen in einer Darstellungsebene auf die anderen Darstellungsebenen aufgezeigt.<ref>Urff, C.: Kritische Bemerkungen zum Einsatz von Kriterienkatalogen zur Bewertung von Lernsoftware. http://www.lernsoftware-mathematik.de/, Stand: 05.03.2020</ref><ref>Urff, C.: Potentiale und Perspektiven digitaler Lernmedien für die Förderung grundlegender mathematischer Kompetenzen. In Zeitschrift für Heilpädagogik, 2010, Jhg. 61.S. 144.</ref><ref>Walter, D.: Nutzungsweisen bei der Verwendung von Tablet-Apps. Dissertation, 2018, S. 43-51 ISBN 3658190671.</ref>
#*Enaktive, ikonische und symbolische Darstellungen eines fachlichen Inhalts können interaktiv verknüpft werden (bspw. mit Multi-Touch-Funktion <ref>Walter, D.: Nutzungsweisen bei der Verwendung von Tablet-Apps. Dissertation, 2018, S. 56-62, ISBN 3658190671.</ref><ref>Drijvers, P.: Head in the clouds, feet in the ground – A realistic view on using digital tools in mathematics education. In (Büchter, A.; Glade, M.; Herold-Blasius, R. Hrsg.): Vielfältige Zugänge zum Mathematikunterricht. Konzepte und Beispiele aus Forschung und Praxis, 2019, S. 173, ISBN 3658242922.</ref>). Dabei werden die Auswirkungen der Änderungen in einer Darstellungsebene auf die anderen Darstellungsebenen aufgezeigt.<ref>Urff, C.: Kritische Bemerkungen zum Einsatz von Kriterienkatalogen zur Bewertung von Lernsoftware. http://www.lernsoftware-mathematik.de/, Stand: 05.03.2020</ref><ref>Urff, C.: Potentiale und Perspektiven digitaler Lernmedien für die Förderung grundlegender mathematischer Kompetenzen. In Zeitschrift für Heilpädagogik, 2010, Jhg. 61.S. 144.</ref><ref>Walter, D.: Nutzungsweisen bei der Verwendung von Tablet-Apps. Dissertation, 2018, S. 43-51 ISBN 3658190671.</ref>
#*Enaktive, ikonische und symbolische Darstellungen eines fachlichen Inhalts werden durch eine getalterische Vielfalt mit einander verknüpft.
#*Enaktive, ikonische und symbolische Darstellungen eines fachlichen Inhalts werden durch eine gestalterische Vielfalt mit einander verknüpft.


===Graduierung===
===Graduierung===

Version vom 11. August 2020, 09:36 Uhr

Steckbrief
Name Datstellungswechsel
Dimension technologisch
Notwendigkeit für das Szenario obligatorisch
Messbarkeit absolut

Werden die fachlichen Inhalte des digitalen Mediums auf allen drei Ebenen des Brunerschen EIS-Prinzips dargestellt, so erfüllt dieses Medium das Kriterium des Darstellungswechsels. Der Lerngegenstand kann mit Hilfe dreier Ebenen dargestellt werden: der Enaktiven (Handlungsebene), der Ikonischen (Bildebene) und der Symbolisch/Formalen (Zeichenebene)[1]. Das digitale Medium sollte möglichst alle drei Formen der Darstellungen anbieten [2], da so kohärente Darstellungen des Lerngegenstandes entwickelt werden können, die inhaltliche Transferleistungen ermöglichen. Hierbei ist es wichtig, dass die Darstellungsebenen untereinander nicht vermischt werden. Handlungen, die digital vollzogen werden, nennt man auch virtuell enaktiv [3].

Kriterium

Das digitale Medium stellt den fachlichen Inhalt auf allen drei Darstellungsebenen des Brunerschen EIS-Prinzips dar und ermöglicht eine Verknüpfung der Ebenen miteinander.

Beschreibung

Zu prüfende Merkmale

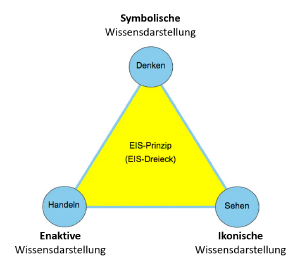
Die drei Ebenen des Brunerschern EIS-Prinzips[4]
  1. Zu prüfende notwendige Merkmale hinsichtlich des EIS-Prinzips sind:
    • Der fachliche Inhalt wird auf der enaktiven Ebene dargestellt.
    • Der fachliche Inhalt wird auf der ikonischen Ebene dargestellt.
    • Der fachliche Inhalt wird auf der symbolisch/formalen Ebene dargestellt.
  2. Zu prüfende Merkmale hinsichtlich der Verknüpfung sind:
    • Enaktive, ikonische und symbolische Darstellungen eines fachlichen Inhalts können interaktiv verknüpft werden (bspw. mit Multi-Touch-Funktion [5][6]). Dabei werden die Auswirkungen der Änderungen in einer Darstellungsebene auf die anderen Darstellungsebenen aufgezeigt.[7][8][9]
    • Enaktive, ikonische und symbolische Darstellungen eines fachlichen Inhalts werden durch eine gestalterische Vielfalt mit einander verknüpft.

Graduierung

Beschreibung
Stufe 0 Das digitale Medium enthält nur eine der drei Darstellungsebenen.
Stufe 1 Das digitale Medium enthält nur ein Teil der Darstellungsebenen, aber nur ein Teil von ihnen kann interaktiv verknüpft werden.
Stufe 2 Das digitale Medium enthält alle Merkmale, d.h. alle Darstellungsebenen sind enthalten, und eine interaktive Verknüpfung zwischen allen Ebenen ist möglich.

Weiterführende Hinweise

  • Sollten mehrere Medien gemeinsam, in einem zeitlich, räumlich, methodisch/didaktischem Zusammenhang, für die Darstellungsebenen genutzt werden, ist dem EIS-Prinzip ebenfalls genüge getan.
  • Explizites Verknüpfen von verschiedenen Darstellungsebenen hat sich als förderlich für das mentale Nachkonstruieren von Zusammenhängen zwischen Darstellungsebenen herausgestellt.[10]
  • Die Technologie bietet die Möglichkeit, mit mehreren, dynamisch verknüpften Darstellungsebenen zu arbeiten. [11]
  • In der Literatur wird im EIS-Prinzip zwischen “virtuell-enaktiv” und “echt-enaktiv” unterschieden. [12]
  • Das Medium sollte die Ausbildung und das mentale Operieren von/mit Vorstellungsbildern unterstützen. D.h. dass das Medium dabei hilft, eine Vorstellung über einen "abstrakten mathematischen Begriff" auszubilden. Beispiel: Wenn der Ausdruck ein Viertel gehört wird (symbolischen Ebene), wird eine viertel Pizza vorgestellt (ikonischen Ebene). Und die viertel Pizza "im Kopf" ist das (mentale) Vorstellungsbild. Dies kann mittels des Lernfortschrittsmonitoring geprüft werden.

Praxisbeispiel (Stufe 1)

Prototyp eines in Augmented Reality dargestellten Insertionsort-Algorithmus
Prototyp einer digitalen Waage zum Sortieren von "Blackbox"-Gewichten

Für die Vermittlung von Sortieralgorithmen im Informatikunterricht nutzt die Lehrkraft eine Tablet-App. In dieser werden dreidimensionale Säulen (ikonische Ebene) in Augmented Reality dargestellt, die nach einem bestimmten Algorithmus sortiert werden. Neben möglichen interaktiven Komponenten, wie der Zeitmanipulation oder der Eingabe von Werten, haben die Lernenden gleichzeitig die Möglichkeit (interaktive Verknüpfung), die entsprechende Programmcodezeile hervorgehoben zu betrachten (symbolische Ebene). Die schrittweise Ausführung des Algorithmus kann daher sowohl auf der ikonischen, als auch auf der symbolischen Ebene analysiert werden. Zusätzlich wird in der App eine digitale Waage genutzt, mit der die Lernenden den gleichen Algorithmus selbst, in der Rolle des Computers, durchführen können (enaktive Ebene).

Einzelnachweise

  1. ↑ Bruner, J.: The Process of Education. Cambridge: Harvard University Press, 1966, S.34-38 ISBN: 9780674710009
  2. ↑ Kalbitz, M.; Voss, H.; Schulte, C. (2011): Informatik begreifen – Zur Nutzung von Veranschaulichungen im Informatikunterricht. In: M. Thomas (Hg.): Informatik in Bildung und Beruf. Unter Mitarbeit von INFOS 2011. Bonn: Gesellschaft für Informatik e.V., S. 137–146.
  3. ↑ Walter, D.: Nutzungsweisen bei der Verwendung von Tablet-Apps. Dissertation, 2018, S.33. ISBN 3658190671.
  4. ↑ Berger, P.: Einführung in die Mathematikdidaktik, Abgerufen auf: www.prof-dr-berger.de/pdf/BergerEinfMathDidaktik.pdf, S.18, Stand: 02.04.2017.
  5. ↑ Walter, D.: Nutzungsweisen bei der Verwendung von Tablet-Apps. Dissertation, 2018, S. 56-62, ISBN 3658190671.
  6. ↑ Drijvers, P.: Head in the clouds, feet in the ground – A realistic view on using digital tools in mathematics education. In (Büchter, A.; Glade, M.; Herold-Blasius, R. Hrsg.): Vielfältige Zugänge zum Mathematikunterricht. Konzepte und Beispiele aus Forschung und Praxis, 2019, S. 173, ISBN 3658242922.
  7. ↑ Urff, C.: Kritische Bemerkungen zum Einsatz von Kriterienkatalogen zur Bewertung von Lernsoftware. http://www.lernsoftware-mathematik.de/, Stand: 05.03.2020
  8. ↑ Urff, C.: Potentiale und Perspektiven digitaler Lernmedien für die Förderung grundlegender mathematischer Kompetenzen. In Zeitschrift für Heilpädagogik, 2010, Jhg. 61.S. 144.
  9. ↑ Walter, D.: Nutzungsweisen bei der Verwendung von Tablet-Apps. Dissertation, 2018, S. 43-51 ISBN 3658190671.
  10. ↑ Walter, D.: Nutzungsweisen bei der Verwendung von Tablet-Apps. Dissertation, 2018, S. 46, ISBN 3658190671.
  11. ↑ Trgalová, J.; Clark-Wilson, A.; Weigand, H.-G.: Technology and resources in mathematics education. In (Dreyfus, Tommy. and Artigue, Michele. and Potari, Despina. and Prediger, Susanne. and Ruthven, Kenneth. Hrsg.): Developing Research in Mathematics Education : Twenty Years of Communication, Cooperation and Collaboration in Europe. Routledge, London, 2018.S. 145. ISBN 1138080292.
  12. ↑ Walter, D.: Nutzungsweisen bei der Verwendung von Tablet-Apps. Dissertation, 2018, S. 33, ISBN 3658190671.
Abgerufen von „https://wiki.sachsen.schule/digit/index.php?title=Darstellungswechsel&oldid=1616“