Strukturieren von Mengen: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 8: | Zeile 8: | ||
[[Simultanes Erfassen]] unstrukturierter Mengen erreicht schnell seine Grenzen. Mehr als vier bis fünf Objekte können nur selten gleichzeitig erfasst werden. Strukturiert man sie, lassen sich auch große Mengen leicht erfassen. | [[Simultanes Erfassen]] unstrukturierter Mengen erreicht schnell seine Grenzen. Mehr als vier bis fünf Objekte können nur selten gleichzeitig erfasst werden. Strukturiert man sie, lassen sich auch große Mengen leicht erfassen. | ||
__INHALTSVERZEICHNIS_ERZWINGEN__ | __INHALTSVERZEICHNIS_ERZWINGEN__ | ||
| Zeile 64: | Zeile 67: | ||
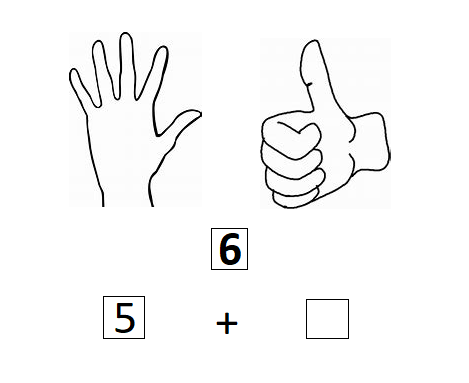
Bei dieser Aufgabe werden sich die Hände als vertrautes Medium zunutze gemacht. Die Kinder können meist | Bei dieser Aufgabe werden sich die Hände als vertrautes Medium zunutze gemacht. Die Kinder können meist schon simultan die Anzahl der Finger erfassen. Anschließend soll, auf Grundlage der Bedeutung der Zahl Fünf, die Zerlegung der Zahl Sechs geübt werden. | ||
[[Datei:Aufgabe1.png]] | [[Datei:Aufgabe1.png]] | ||
Aktuelle Version vom 21. Januar 2020, 13:05 Uhr
Der Inhalt dieser Seite bezieht sich auf das Thema "Strukturieren von Mengen mit bis zu 100 Elementen" des Teilbereichs "Einblick gewinnen in die Zahlenwelt" aus dem sächsischen Lehrplan.
Im Mathematikunterricht spielen das Erfassen von Anzahlen und damit auch Strukturierungshilfen zur schnellen Anzahlerfassung eine wichtige Rolle.
Simultanes Erfassen unstrukturierter Mengen erreicht schnell seine Grenzen. Mehr als vier bis fünf Objekte können nur selten gleichzeitig erfasst werden. Strukturiert man sie, lassen sich auch große Mengen leicht erfassen.
Strukturierungshilfen im Zahlenraum bis 10
Die Zahl Fünf spielt eine bedeutende Rolle in der Arithmetik. Sie ist die größte Menge, die ungeordnet simultan erfasst werden kann. Darüber hinaus ist sie eine große Hilfe zum Strukturieren und Erfassen größerer Anzahlen. Es kann daher besonders für den Anfang Sinn machen, die Zahlen Sechs bis Zehn zur Zahl Fünf in Beziehung zu setzen und sie als Zerlegung 5 + x darzustellen.
- Würfelbilder für die Megen bis 6
Die meisten Kinder sind durch ihren Alltag mit Würfelbildern vertraut. Sie sehen daher sofort, dass auf diesen Würfeln die Zahlen Fünf und Eins gezeigt werden, ohne dass sie zählen müssen.
- die Hände
-
Die Hand zeigt die Zahl Drei.
-
Die Hand zeigt die Zahl Fünf.
Anfangs zählen Kinder mit den Fingern, jedoch lernen sie schnell, dass bspw. eine volle Hand die Zahl Fünf verkörpert. Dann müssen sie nicht mehr zählen.
- Bündelungen in Fünfer- oder Zehnergruppen
Kinder können Anzahlen schneller erfassen, wenn die Mengen zuvor gebündelt wurden. Bei diesem Beispiel erkennt man durch die Fünferbündelung nun schnell, dass hier die Zahl Acht abgebildet wird.
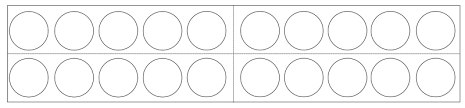
- das Zehnerfeld
Das Zehnerfeld ist ein zentrales arithmetisches Arbeitsmittel.Es besteht aus zwei nebeneinander angeordneten Reihen mit je fünf Feldern, die eine schnelle Orientierung ermöglichen.
- Beispielaufgaben
Bei dieser Aufgabe werden sich die Hände als vertrautes Medium zunutze gemacht. Die Kinder können meist schon simultan die Anzahl der Finger erfassen. Anschließend soll, auf Grundlage der Bedeutung der Zahl Fünf, die Zerlegung der Zahl Sechs geübt werden.
Bei dieser Aufgabe wird anfänglich nur das erste Feld, in diesem Fall die Zahl Sechs, vorgegeben. Anschließend soll die Sechs dann als Strichliste, im Zehnerfeld und als Zerlegung/Additionsaufgabe dargestellt werden. Dabei soll immer wieder durch farbige Markierungen die Zahl Sechs mit der besonderen Zahl Fünf in Beziehung gesetzt werden.
Strukturierungshilfen im Zahlenraum bis 100
- das Zwanzigerfeld
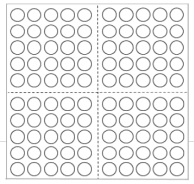
- das Hunderterfeld
Das Zwanziger- und das Hunderterfeld sind Erweiterungen des Zehnerfeldes. Bei allen Felder macht man sich die Fünfer- und Zehnerbündelung zunutze. Am Hunderterfeld kann man durch die Struktur auch gut die Fünfzig erkennen. Die Felder kann man gut zum Legen von Zahlen verwenden, diese aber auch durch das Ausmalen von Feldern darstellen. Davon ausgehend kann man dann mit der Einführung der Stellenwerttafel beginnen.
Literatur
- Autor: Frank Lippmann Nussknacker 1. Mein Mathebuch. Klett Verlag, 2015, 978-3-12-254510-9 .
- Autor: Frank Lippmann Nussknacker 2. Mein Mathebuch. Klett Verlag, 2015, 978-3-12-254520-8 .