Halbieren: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (12 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Unter dem Begriff [[Halbieren]] versteht man, dass ein Gegenstand oder ein Körper in zwei gleich große Teile geteilt wird bzw. dieser um die Hälfte verringert wird. | |||
Im nachfolgendem Artikel soll es nun um das [[Halbieren]] im geometrischem Sinne gehen. | |||
== Verbindung zum Halbieren bei einer Spiegelung == | == Verbindung zum Halbieren bei einer Spiegelung == | ||
'''Verbindung zum Halbieren einer Spiegelung als Abbildung'''ist ein Teilgebiet des sächsischen Lehrplans Sachsen im Bereich der Geometrie. Vorgesehen ist dieser in der Klassenstufe 1/2. | '''Verbindung zum Halbieren einer Spiegelung als Abbildung'''ist ein Teilgebiet des sächsischen Lehrplans Sachsen im Bereich der Geometrie. Vorgesehen ist dieser in der Klassenstufe 1/2. | ||
| Zeile 4: | Zeile 7: | ||
== Grundlegende Definitionen == | == Grundlegende Definitionen == | ||
Unter einer [[Spiegelung]] versteht man eine umgedrehte [[Abbildung]] eines Gegenstands, welche mit Hilfe eines Spiegels erzeugt wird. Dafür gibt es eine [[Spiegelachse]], an welcher man den [[Spiegel]] anlegt. Dabei gibt es den besonderen Fall der „[[Symmetrie]]“. | Unter einer [[Spiegelung]] versteht man eine umgedrehte [[Abbildung]] eines Gegenstands, welche mit Hilfe eines Spiegels erzeugt wird. Dafür gibt es eine [[Spiegelachse]], an welcher man den [[Spiegel]] anlegt. Dabei gibt es den besonderen Fall der „[[Symmetrie]]“. Ist dies der Fall, so sprechen wie von einer [[achsensymmetrisch]]en Figur. | ||
Unter dem Begriff „Halbieren“ versteht man, dass man von einem ganzen Gegenstand oder einer Menge, genau die Hälfte weggenommen wird. | Unter dem Begriff „Halbieren“ versteht man, dass man von einem ganzen Gegenstand oder einer Menge, genau die Hälfte weggenommen wird. | ||
Wenn man nun die [[Spiegelung]] mit dem Halbieren in Verbindung bringen will, so muss man sich zunächst einen symmetrischen Körper suchen. Stellt man nun einen Spiegel auf die [[Symmetrieachse]] oder deckt die eine Hälfte des Körpers hab, so hat man diesen halbiert. | Wenn man nun die [[Spiegelung]] mit dem Halbieren in Verbindung bringen will, so muss man sich zunächst einen symmetrischen Körper suchen. Stellt man nun einen Spiegel auf die [[Symmetrieachse]] oder deckt die eine Hälfte bis zur [[Spiegelachse]] des Körpers hab, so hat man diesen halbiert. Anders herum bedeutet dies: Wenn man eine Hälfte eines Körpers hat und an dessen Rand einen Spiegel anlegt, so wird diese Figur verdoppelt. | ||
== Einige Beispiele == | == Einige Beispiele == | ||
| Zeile 13: | Zeile 16: | ||
*Das folgende Arbeitsblatt 1 zeigt jeweils die Hälfte einer Figur. Mit Hilfe eines Spiegels und der [[Symmetrie]] sollst du nun die zweite Hälfte noch ergänzen. | *Das folgende Arbeitsblatt 1 zeigt jeweils die Hälfte einer Figur. Mit Hilfe eines Spiegels und der [[Symmetrie]] sollst du nun die zweite Hälfte noch ergänzen. | ||
[[Datei:Symmetrie1.png| | [[Datei:Symmetrie1.png|300px]] | ||
Quelle: https://www.grundschulkoenig.de/mathe/3-klasse/symmetrie/ | |||
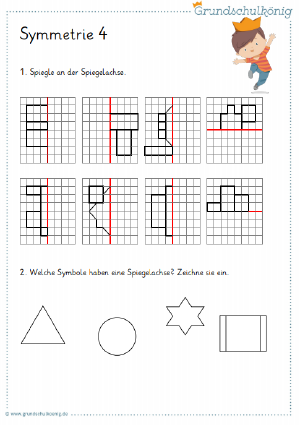
*In einer zweiten Beispielaufgabe (siehe Arbeitsblatt 2) soll man nun die [[Spiegelachse]] finden. Die Beispiele sind so gewählt, dass man genau die Hälfte der Figur finden muss. Überprüfen kann man die eigene Lösung mit Hilfe eines Spiegels, den man an die [[Spiegelachse]] anlegen sollte. | *In einer zweiten Beispielaufgabe (siehe Arbeitsblatt 2) soll man nun die [[Spiegelachse]] finden. Die Beispiele sind so gewählt, dass man genau die Hälfte der Figur finden muss. Überprüfen kann man die eigene Lösung mit Hilfe eines Spiegels, den man an die [[Spiegelachse]] anlegen sollte. | ||
[[Datei:Symmetrie2.jpg| | [[Datei:Symmetrie2.jpg|300px]] | ||
Quelle: https://www.grundschulkoenig.de/mathe/4-klasse/symmetrie-symmetrieachse-symmetrische-figuren/ | |||
== Bezug zum sächsischen Lehrplan == | == Bezug zum sächsischen Lehrplan == | ||
Aktuelle Version vom 18. März 2020, 10:09 Uhr
Unter dem Begriff Halbieren versteht man, dass ein Gegenstand oder ein Körper in zwei gleich große Teile geteilt wird bzw. dieser um die Hälfte verringert wird. Im nachfolgendem Artikel soll es nun um das Halbieren im geometrischem Sinne gehen.
Verbindung zum Halbieren bei einer Spiegelung
Verbindung zum Halbieren einer Spiegelung als Abbildungist ein Teilgebiet des sächsischen Lehrplans Sachsen im Bereich der Geometrie. Vorgesehen ist dieser in der Klassenstufe 1/2.
Grundlegende Definitionen
Unter einer Spiegelung versteht man eine umgedrehte Abbildung eines Gegenstands, welche mit Hilfe eines Spiegels erzeugt wird. Dafür gibt es eine Spiegelachse, an welcher man den Spiegel anlegt. Dabei gibt es den besonderen Fall der „Symmetrie“. Ist dies der Fall, so sprechen wie von einer achsensymmetrischen Figur. Unter dem Begriff „Halbieren“ versteht man, dass man von einem ganzen Gegenstand oder einer Menge, genau die Hälfte weggenommen wird.
Wenn man nun die Spiegelung mit dem Halbieren in Verbindung bringen will, so muss man sich zunächst einen symmetrischen Körper suchen. Stellt man nun einen Spiegel auf die Symmetrieachse oder deckt die eine Hälfte bis zur Spiegelachse des Körpers hab, so hat man diesen halbiert. Anders herum bedeutet dies: Wenn man eine Hälfte eines Körpers hat und an dessen Rand einen Spiegel anlegt, so wird diese Figur verdoppelt.
Einige Beispiele
- Das folgende Arbeitsblatt 1 zeigt jeweils die Hälfte einer Figur. Mit Hilfe eines Spiegels und der Symmetrie sollst du nun die zweite Hälfte noch ergänzen.
Quelle: https://www.grundschulkoenig.de/mathe/3-klasse/symmetrie/
- In einer zweiten Beispielaufgabe (siehe Arbeitsblatt 2) soll man nun die Spiegelachse finden. Die Beispiele sind so gewählt, dass man genau die Hälfte der Figur finden muss. Überprüfen kann man die eigene Lösung mit Hilfe eines Spiegels, den man an die Spiegelachse anlegen sollte.
Quelle: https://www.grundschulkoenig.de/mathe/4-klasse/symmetrie-symmetrieachse-symmetrische-figuren/
Bezug zum sächsischen Lehrplan
Klassenstufe 1/2, Lernbereich 1: Geometrie - Einblick gewinnen in die Spiegelung als Abbildung (Verbindung zum Halbieren)