Strahensätze: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Unter den Strahlensätzen werden in der ebenen [[Geometrie]] Zusammenhänge über die Streckenlängen an geschnittenen Parallelen zusammengefasst. | Unter den Strahlensätzen werden in der ebenen [[Geometrie]] Zusammenhänge über die Streckenlängen an geschnittenen Parallelen zusammengefasst. | ||
Die in den folgenden Erklärungen verwendeten geometrischen Bezeichnungen beziehen sich dabei auf das Bild am rechten Rand. | |||
=Erster Strahlensatz= | =Erster Strahlensatz= | ||
| Zeile 31: | Zeile 32: | ||
# Beschreibe, warum die Umkehrung des zweiten Strahlensatzes im Allgemeinen nicht gilt! | # Beschreibe, warum die Umkehrung des zweiten Strahlensatzes im Allgemeinen nicht gilt! | ||
# In welchem Fall sind die beiden Varianten der Strahlensätze gleichzusetzen? | # In welchem Fall sind die beiden Varianten der Strahlensätze gleichzusetzen? | ||
[[Kategorie: Geometrie]] | |||
Aktuelle Version vom 19. September 2020, 14:54 Uhr
Unter den Strahlensätzen werden in der ebenen Geometrie Zusammenhänge über die Streckenlängen an geschnittenen Parallelen zusammengefasst. Die in den folgenden Erklärungen verwendeten geometrischen Bezeichnungen beziehen sich dabei auf das Bild am rechten Rand.
Erster Strahlensatz
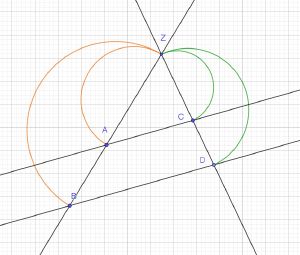
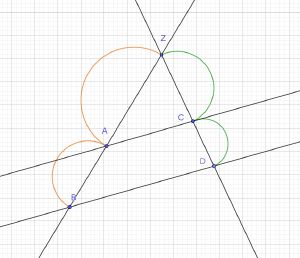
Wenn zwei Strahlen mit gemeinsamen Anfangspunkt von zwei Parallelen geschnitten werden, dann gelten für die dabei entstehenden Teilstrecken folgende Beziehungen:
- Die Strecke ZA verhält sich zur Strecke ZB genauso, wie die Strecke ZC zur Strecke ZD.
- ZA:ZB=ZC:ZD
- Die Strecke ZA verhält sich zur Strecke AB genauso, wie die Strecke ZC zur Strecke CD.
- ZA:AB=ZC:CD
Umkehrung
Zwei Strahlen mit einem gemeinsamen Anfangspunkt werden von zwei Geraden geschnitten. Wenn für die Teilstrecken gilt
- ZA:ZB=ZC:ZD
so sind die beiden Geraden parallel zueinander.
Zweiter Strahlensatz
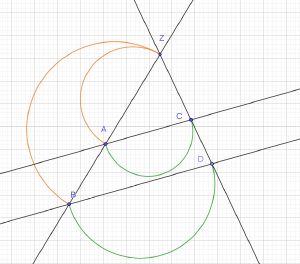
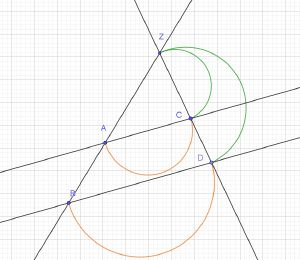
Auch beim Zweiten Strahlensatz gilt: Wenn zwei Strahlen mit gemeinsamen Anfangspunkt von zwei Parallelen geschnitten werden, dann gelten für die dabei entstehenden Teilstrecken folgende Beziehungen:
- Die Strecke AC verhält sich zur Strecke BD genauso, wie die Strecke ZA zur Strecke ZB.
- AC:BD=ZA:ZB
- Die Strecke AC verhält sich zur Strecke BD genauso, wie die Strecke ZC zur Strecke ZD.
- AC:BD=ZC:ZD
Weiterführende Aufgaben
- Beschreibe, warum die Umkehrung des zweiten Strahlensatzes im Allgemeinen nicht gilt!
- In welchem Fall sind die beiden Varianten der Strahlensätze gleichzusetzen?