Peripherie – Zentriwinkel – Satz: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
In der Geometrie gibt es einige Zusammenhänge zwischen verschiedenen [[Winkeln]] in [[Kreisen]]. So auch zwischen '''Peripheriewinkel''' und '''Zentriwinkel'''. Diese Kreiswinkelbeziehung sagt aus, dass der Zentriwinkel halb so groß wie der Peripheriewinkel ist. | |||
= | = Erklärung = | ||
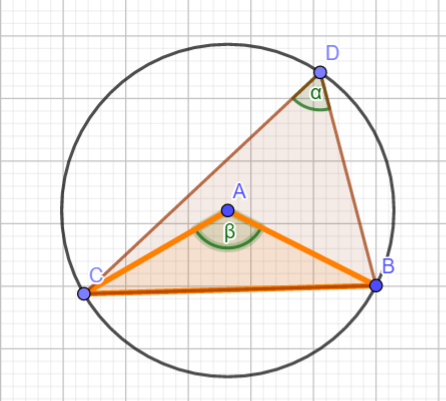
Die über einem Bogen und einer Sehne liegenden '''Peripheriewinkel''' eines Kreises sind untereinander gleich und halb so groß wie der zugehörige '''Zentriwinkel'''. | Die über einem Bogen und einer Sehne liegenden '''Peripheriewinkel''' eines Kreises sind untereinander gleich und halb so groß wie der zugehörige '''Zentriwinkel'''. | ||
Der '''Peripheriewinkel''' | Der '''Peripheriewinkel''' ist in der Skizze der Winkel Alpha α. Winkel Beta β ist der Zentriwinkel. | ||
Demzufolge ist die Aussage: ''α = β/2'' | Demzufolge ist die Aussage: ''α = β/2''. Dies trifft im Allgemeinen Fall zu und gilt für alle Peripheriewinkel über dem gleichen Kreisbogen zu. | ||
[[Datei:Peripeherie-Zentri-Winkel.png]] | [[Datei:Peripeherie-Zentri-Winkel.png]] | ||
= Satz des Thales = | = Satz des Thales = | ||
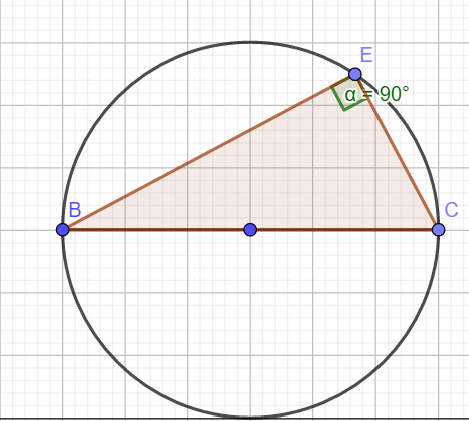
Ein Spezialfall ist der '''Satz des Thales'''. Ist die Sehne der Durchmesser des Kreises, so ist der Peripheriewinkel 90 Grad. | Ein Spezialfall ist der '''Satz des Thales'''. Ist die Sehne der Durchmesser des Kreises, so ist der Peripheriewinkel 90 Grad, da der Zentriwinkel 180 Grad ist. | ||
[[Datei:Satz des Thales.png]] | [[Datei:Satz des Thales.png]] | ||
= Anwendung = | = Anwendung = | ||
Diese Winkelbeziehung wichtig für die Konstruktion verschiedener technischer Sachverhalte. Zum Beispiel bei der Konstruktion von Polygonen. Dort kann man mit Hilfe der Winkelbeziehungen Zwanzigecke oder Fünfzigecke konstruieren. | |||
[[Kategorie: Geometrie]] | [[Kategorie: Geometrie]] | ||
Aktuelle Version vom 26. September 2020, 07:38 Uhr
In der Geometrie gibt es einige Zusammenhänge zwischen verschiedenen Winkeln in Kreisen. So auch zwischen Peripheriewinkel und Zentriwinkel. Diese Kreiswinkelbeziehung sagt aus, dass der Zentriwinkel halb so groß wie der Peripheriewinkel ist.
Erklärung
Die über einem Bogen und einer Sehne liegenden Peripheriewinkel eines Kreises sind untereinander gleich und halb so groß wie der zugehörige Zentriwinkel. Der Peripheriewinkel ist in der Skizze der Winkel Alpha α. Winkel Beta β ist der Zentriwinkel. Demzufolge ist die Aussage: α = β/2. Dies trifft im Allgemeinen Fall zu und gilt für alle Peripheriewinkel über dem gleichen Kreisbogen zu.
Satz des Thales
Ein Spezialfall ist der Satz des Thales. Ist die Sehne der Durchmesser des Kreises, so ist der Peripheriewinkel 90 Grad, da der Zentriwinkel 180 Grad ist.
Anwendung
Diese Winkelbeziehung wichtig für die Konstruktion verschiedener technischer Sachverhalte. Zum Beispiel bei der Konstruktion von Polygonen. Dort kann man mit Hilfe der Winkelbeziehungen Zwanzigecke oder Fünfzigecke konstruieren.