Magische Quadrate: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (5 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 25: | Zeile 25: | ||
Weiterhin kann das magische Quadrat abgewandelt werden, indem die Zauberzahl oder die Summe vorgegeben wird. | Weiterhin kann das magische Quadrat abgewandelt werden, indem die Zauberzahl oder die Summe vorgegeben wird. | ||
<gallery mode="packed-hover" caption="Beispiele" style="max-width:300px"> | |||
Beispiel2.jpg|Beispiel 1 | |||
Beispiel3 .jpg|Beispiel 2 <ref>https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/Haus_7_-_Gute_-_Aufgaben/IM/Informationstexte/H7_IM_Zauberquadrate.pdf | |||
Beispiel 4.jpg|Beispiel 3 <ref>https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/Haus_7_-_Gute_-_Aufgaben/IM/Informationstexte/H7_IM_Zauberquadrate.pdf | |||
</gallery> | |||
== magische Quadrate im Mathematikunterricht == | == magische Quadrate im Mathematikunterricht == | ||
| Zeile 44: | Zeile 40: | ||
*Vergleiche die Mittelzahl und die Zauberzahl miteinander! | *Vergleiche die Mittelzahl und die Zauberzahl miteinander! | ||
*Erfinde selbst magische Quadrate! | *Erfinde selbst magische Quadrate! | ||
== Kompetenzerwartungen == | == Kompetenzerwartungen == | ||
| Zeile 62: | Zeile 50: | ||
== Lehrplanbezug == | == Lehrplanbezug == | ||
Magische Quadrate können in verschiedenen Klassenstufen eingesetzt werden: | Magische Quadrate können in verschiedenen Klassenstufen eingesetzt und entsprechend angepasst werden: | ||
*'''Klasse 1/ 2''': ''Wahlbereich'' 2 | *'''Klasse 1/ 2''': ''Wahlbereich'' 2 | ||
| Zeile 82: | Zeile 70: | ||
<ref>http://lpdb.schule-sachsen.de/lpdb/web/downloads/10_lp_gs_mathematik_2019.pdf?v2</ref> | <ref>http://lpdb.schule-sachsen.de/lpdb/web/downloads/10_lp_gs_mathematik_2019.pdf?v2</ref> | ||
== Übung == | |||
*1.Löse nun selbst ein magisches Quadrat! | |||
*2. Was passiert, wenn die Zauberzahl halbiert wird? Begründe! | |||
*3. Erstelle selbst ein magisches Quadrat! (3x3 Gitter) | |||
[[Datei:Beispiel1.jpg]] | |||
== Literatur == | == Literatur == | ||
| Zeile 87: | Zeile 82: | ||
PIKAS DEUTSCHES ZENTRUM FÜR LEHRBILDUNG MATHEMATIK (2010). Zauberquadrate | PIKAS DEUTSCHES ZENTRUM FÜR LEHRBILDUNG MATHEMATIK (2010). Zauberquadrate | ||
entdecken.<ref>https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/Haus_7_-_Gute_- | entdecken. | ||
_Aufgaben/IM/Informationstexte/H7_IM_Zauberquadrate.pdf</ref> | <ref>https://pikas.dzlm.de/pikasfiles/uploads/upload/Material/Haus_7_-_Gute_-_Aufgaben/IM/Informationstexte/H7_IM_Zauberquadrate.pdf</ref> | ||
SÄCHSISCHES STAATSINSTITUT FÜR BILDUNG UND SCHULENTWICKLUNG (2019). Lehrplan | SÄCHSISCHES STAATSINSTITUT FÜR BILDUNG UND SCHULENTWICKLUNG (2019). Lehrplan | ||
Grundschule.Mathematik. | Grundschule.Mathematik. | ||
<ref>https://www.schule.sachsen.de/lpdb/web/downloads/10_lp_gs_mathematik_2019.pdf</ref> | <ref>https://www.schule.sachsen.de/lpdb/web/downloads/10_lp_gs_mathematik_2019.pdf</ref> | ||
Aktuelle Version vom 23. März 2021, 08:30 Uhr
Das magische Quadrat, auch Zauberquadrat genannt, ist ein Aufgabenformat des aktiv- entdeckenden Lernens. Hierbei kann neben der Addition und Subtraktion auch eine Erweiterung zur Multiplikation und Division integriert werden. Das magische Quadrat ist in der Regel ein 3x3 Gitter, bei welchem die waagerechten, senkrechten und diagonalen Zahlen die gleiche Summe aufweisen.
Allgemeiner Aufbau
Magische Quadrate werden auch Zauberquadrate genannt und sind mathematische Aufgaben. Sie existieren für alle natürlichen Zahlen n>2.
Im Regelfall bestehen sie jedoch aus einem Gitter, welches drei Spalten und drei Zeilen enthält.
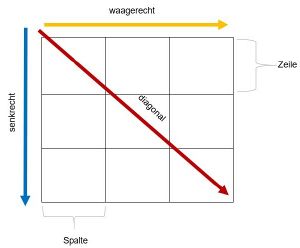
Dabei sind in einigen Zellen verschiedene Zahlen vorgegeben und andere sind ausgespart. Wurden die Zauberquadrate gelöst, so befinden sich in jeder Zeile sowie Spalte jeweils drei Zahlen. Besonders hierbei ist, dass die drei waagerechten, senkrechten sowie diagonalen Zahlen jeweils addiert werden und die gleiche Summe enthalten. Diese Summe der magischen Quadrate wird als sogenannte Zauberzahl bezeichnet. Bei einem 3x3 Zauberquadrat entspricht diese der dreifachen Zahl, welche in der Mitte des Quadrats steht.
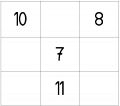
-
magisches Quadrat mit freien Feldern
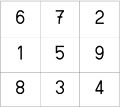
-
ausgefülltes magisches Quadrat
Bei den magischen Quadraten sind keine Rechenzeichen oder Rechenoperationen vorzufinden. Somit müssen die SchülerInnen eigenständig die entsprechende Rechenart herausfinden, um das Zauberquadrat lösen zu können. Sie werden aktiv- entdeckend tätig. Die entsprechenden Rechnungen müssen sie im Kopf oder auf einem zusätzlichen Blatt lösen.
Erweiterungsmöglichkeiten
Je nach Lernstand und Klassenstufe können magische Quadrate individuell angepasst und eingesetzt werden. Denn, sie sind:
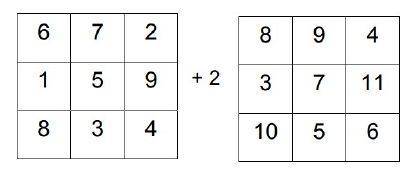
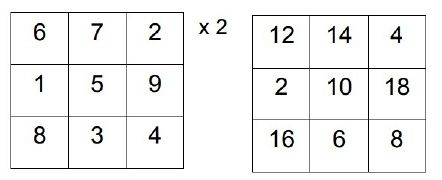
- additiv und multiplikativ veränderbar.
Zudem ist es möglich eine Zeile sowie Spalte hinzuzufügen oder den Zahlenraum zu erweitern. Weiterhin kann das magische Quadrat abgewandelt werden, indem die Zauberzahl oder die Summe vorgegeben wird.
- Beispiele
-
Beispiel 1
magische Quadrate im Mathematikunterricht
mögliche Denkanstöße
- Was fällt dir auf?
- Was fällt dir auf, wenn du die Zeilen, Spalten und Diagonalen betrachtest?
- Warum ist das so?
- Vergleiche die Mittelzahl und die Zauberzahl miteinander!
- Erfinde selbst magische Quadrate!
Kompetenzerwartungen
- Inhaltsbezogene Kompetenzen und prozessbezogene Kompetenzen stehen in engem Zusammenhang:
- beobachten, fragen, vermuten
- entdecken und sprechen über Muster, Gesetzmäßigkeiten, Zahlbeziehungen
- beobachten eigenen operativer Auswirkungen
Lehrplanbezug
Magische Quadrate können in verschiedenen Klassenstufen eingesetzt und entsprechend angepasst werden:
- Klasse 1/ 2: Wahlbereich 2
- Magische Quadrate
- Klasse 1/ 2: Lernbereich 2: Arithmetik
- Beherrschen der Zahlbeziehungen und der Orientierung im Zahlenraum bis 100
- Beherrschen der Grundaufgaben der Addition und Subtraktion im Zahlenraum bis 20
- Klasse 3: Lernbereich 2: Arithmetik
- Beherrschen der Zahlbeziehungen und Orientierung im Zahlenraum bis 1000 und darüber hinaus
- Übertragen der Vorstellungen zur Addition und Subtraktion auf das Rechnen mit Sachverhalten im Zahlenraum bis 1000
- Übertragen des Wissens über Multiplikation und Division auf das Rechnen mit Sachverhalten im Zahlenraum bis 1000
- Klasse 4: Lernbereich 2: Arithmetik
- Kennen des Operierens mit Zahlen bis 1.000.000 und darüber hinaus
- Anwenden des Einspluseins und des kleinen Einmaleins sowie deren Umkehrungen beim Rechnen um Zahlenraum bis 1.000.000 und darüber
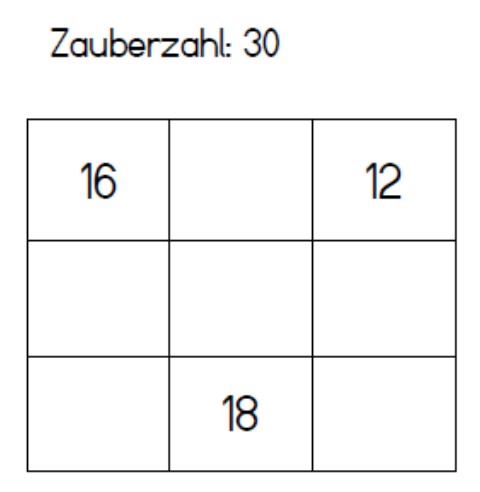
Übung
- 1.Löse nun selbst ein magisches Quadrat!
- 2. Was passiert, wenn die Zauberzahl halbiert wird? Begründe!
- 3. Erstelle selbst ein magisches Quadrat! (3x3 Gitter)
Literatur
PIKAS DEUTSCHES ZENTRUM FÜR LEHRBILDUNG MATHEMATIK (2010). Zauberquadrate entdecken. [2]
SÄCHSISCHES STAATSINSTITUT FÜR BILDUNG UND SCHULENTWICKLUNG (2019). Lehrplan Grundschule.Mathematik. [3]