Mengenbeschreibung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
Dieser Eintrag bezieht sich auf das Thema '''Herstellen der Beziehung von Menge - Zahlwort - Ziffer''' aus dem [https://www.schule.sachsen.de/lpdb/web/downloads/10_lp_gs_mathematik_2019.pdf?v2 sächsischen Lehrplan Mathematik] Klassenstufe 1/2. | Dieser Eintrag bezieht sich auf das Thema '''Herstellen der Beziehung von Menge - Zahlwort - Ziffer''' aus dem [https://www.schule.sachsen.de/lpdb/web/downloads/10_lp_gs_mathematik_2019.pdf?v2 sächsischen Lehrplan Mathematik] Klassenstufe 1/2. | ||
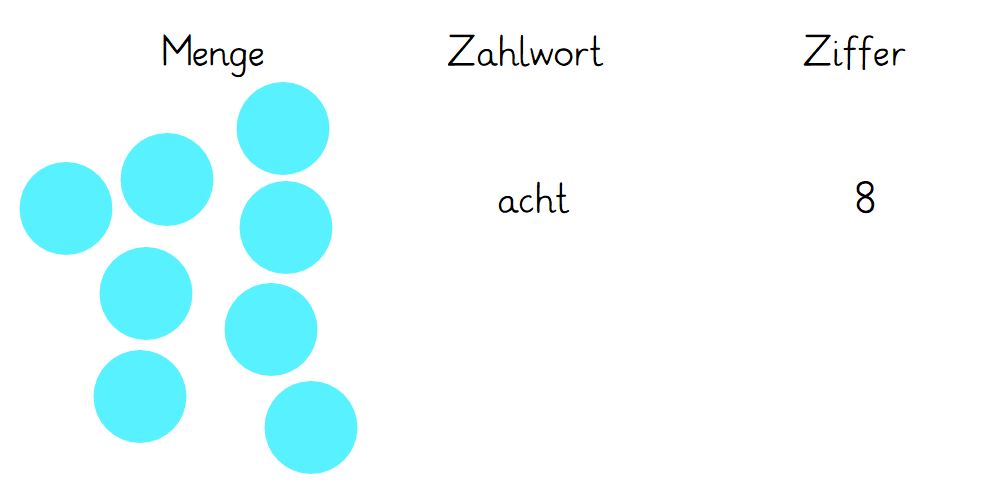
Jede endliche [[Menge]] besitzt eine bestimmte '''Anzahl von Objekten''' (z.B. Würfel, Punkte oder Striche). Diese Anzahl von Objekten kann gezählt und mit genau einem '''Zahlwort''' beschrieben werden. Die jeweiligen [[Zahlwörter]] entsprechen genau einer [[Ziffer]]. | Jede endliche [[Menge]] besitzt eine bestimmte '''Anzahl von Objekten''' (z.B. [[Würfel]], Punkte oder Striche). Diese Anzahl von Objekten kann gezählt und mit genau einem '''Zahlwort''' beschrieben werden. Die jeweiligen [[Zahlwörter]] entsprechen genau einer [[Ziffer]]. | ||
| Zeile 45: | Zeile 45: | ||
Hälst man sich an diese Prinzipien kann jeder Menge genau ein Zahlwort | Hälst man sich an diese Prinzipien kann jeder Menge genau ein Zahlwort zugeordnet werden. Dieses Zahlwort entspricht genau einer Ziffer. | ||
---- | ---- | ||
Aktuelle Version vom 6. Februar 2021, 15:47 Uhr
Dieser Eintrag bezieht sich auf das Thema Herstellen der Beziehung von Menge - Zahlwort - Ziffer aus dem sächsischen Lehrplan Mathematik Klassenstufe 1/2.
Jede endliche Menge besitzt eine bestimmte Anzahl von Objekten (z.B. Würfel, Punkte oder Striche). Diese Anzahl von Objekten kann gezählt und mit genau einem Zahlwort beschrieben werden. Die jeweiligen Zahlwörter entsprechen genau einer Ziffer.
Beispiele
Beispiel 1
Beispiel 2
Beispiel 3
Die Objekte in Beispiel 1 und Beispiel 2 sind unterschiedlich. In beiden Beispielen können jeweils 5 Objekte gezählt werden. Deshalb wird beiden Mengen das Zahlwort fünf und die Ziffer 5 zugeordnet. Während die Anzahl von fünf ungeordneten Objekten noch leicht simultan erfassbar ist, muss die Anzahl der Objekte in Beispiel 3 abgezählt werden.
Zählprinzipien
Um die Anzahl der Objekte richtig zu zählen, müssen folgende Zählprinzipien eingehalten werden:
Eindeutigkeitsprinzip: Jedem zu zählenden Gegenstand wird genau ein Zahlwort zugeordnet.
Prinzip der stabilen Ordnung: Die Reihenfolge der Zählwörter hat eine vorgeschriebene Ordnung (eins, zwei, drei, vier, ...)
Kardinalzahlprinzip: Das zuletzt genannte Zahlwort beim Zählprozess gibt die Anzahl der Objekte der abgezählten Menge an.
Prinzip der Irrelevanz der Anordnung: Die Anordnung der zu zählenden Objekte ist für das Zählergebnis unwichtig.[1]
Hälst man sich an diese Prinzipien kann jeder Menge genau ein Zahlwort zugeordnet werden. Dieses Zahlwort entspricht genau einer Ziffer.
- ↑ Zählprinzipien: Dr. Schulz, Andreas (2019). Wie kommen Kinder zur Zahl? Online im Internet: http://www.luw5.de/pdf/drschulz.pdf