Kreise: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (19 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
=== Mittelpunkt M === | === Mittelpunkt M === | ||
[[Datei:Kreis mit Mittelpunkt M .png|mini|Kreis mit Mittelpunkt M]] | |||
Den Punkt im Kreis, der zu allen Punkten auf der Kreislinie den gleichen Abstand hat, bezeichnet man als '''Mittelpunkt''' des Kreises. Er wird stets mit dem Großbuchstaben '''M''' bezeichnet. | |||
| Zeile 16: | Zeile 27: | ||
=== Radius r === | === Radius r === | ||
[[Datei:Kreis mit Mittelpunkt M und Radius r.png|mini|Kreis mit Mittelpunkt M und Radius r]] | |||
Die Länge der Strecke vom Mittelpunkt M zu einem beliebigen Punkt auf der Kreislinie wird als '''Radius''' bezeichnet. Der Radius ist also der Abstand vom Mittelpunkt zu einem beliebigen Punkt der Kreislinie. Der '''Radius''' wird immer mit dem Kleinbuchstaben '''r''' bezeichnet. | |||
Der '''Durchmesser''' ist die Länge der Strecke zwischen zwei Punkten auf der Kreislinie, die durch den Mittelpunkt M | === Durchmesser d === | ||
[[Datei:Kreis mit Mittelpunkt M und Durchmesser d.png|mini|Kreis mit Mittelpunkt M und Durchmesser d]] | |||
Der '''Durchmesser''' ist die Länge der Strecke zwischen zwei Punkten auf der Kreislinie, die durch den Mittelpunkt M verläuft. Der '''Durchmesser''' wird immer mit dem Kleinbuchstaben '''d''' bezeichnet. | |||
Für den Durchmesser gilt: | Für den Durchmesser gilt: | ||
Verdoppelst du den Radius r, so erhälst du den Durchmesser d, also'''d = 2r''' | Verdoppelst du den Radius r, so erhälst du den Durchmesser d, also: '''d = 2r''' | ||
| Zeile 33: | Zeile 79: | ||
* Uhr | * Uhr | ||
* | * CD | ||
* | * Schallplatte | ||
| Zeile 43: | Zeile 89: | ||
Ein Kreis lässt sich im Alltag auf vielfältige Arten erzeugen. | Ein Kreis lässt sich im Alltag auf vielfältige Arten erzeugen. | ||
So entsteht ein Kreis beispielsweise, wenn | So entsteht ein Kreis beispielsweise, wenn man den Umriss eines zylinderförmigen Gegenstandes, durch Umfahren des Gegenstandes mit einem Stift, auf Papier festhält. | ||
=== Einen Kreis zeichnen === | === Einen Kreis zeichnen === | ||
| Zeile 50: | Zeile 96: | ||
== | == Weblinks == | ||
https://de.serlo.org/mathe/geometrie/dreiecke-vierecke-kreise-andere-ebene-figuren/kreise-kreisteile/kreis | https://de.serlo.org/mathe/geometrie/dreiecke-vierecke-kreise-andere-ebene-figuren/kreise-kreisteile/kreis | ||
| Zeile 58: | Zeile 104: | ||
== Literatur == | == Literatur == | ||
Franke, | Franke, M. & Reinhold, S. (2016). ''Didaktik der Geometrie. In der Grundschule'' (3. Aufl.). Berlin: Springer Spektrum. | ||
[[Kategorie: Geometrie]] | [[Kategorie: Geometrie]] | ||
Aktuelle Version vom 26. Januar 2020, 20:28 Uhr
Als Kreis wird in der Geometrie eine ebene Figur bezeichnet. Dabei hat bei einem Kreis jeder Punkt der Kreislinie den gleichen Abstand vom Mittelpunkt. Kreise werden in der Schule in der Klassenstufe 1/2 unter dem Teilbereich "Übertragen des Wissens über lineare Figuren auf ebene Figuren" im sächsischen Lehrplan behandelt.
Wichtige Begriffe
Mittelpunkt M
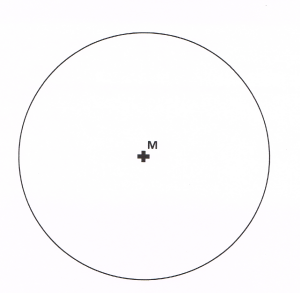
Den Punkt im Kreis, der zu allen Punkten auf der Kreislinie den gleichen Abstand hat, bezeichnet man als Mittelpunkt des Kreises. Er wird stets mit dem Großbuchstaben M bezeichnet.
Radius r
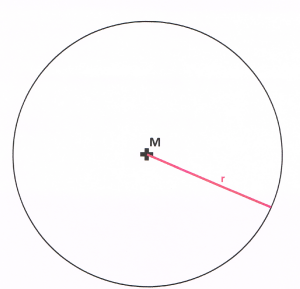
Die Länge der Strecke vom Mittelpunkt M zu einem beliebigen Punkt auf der Kreislinie wird als Radius bezeichnet. Der Radius ist also der Abstand vom Mittelpunkt zu einem beliebigen Punkt der Kreislinie. Der Radius wird immer mit dem Kleinbuchstaben r bezeichnet.
Durchmesser d
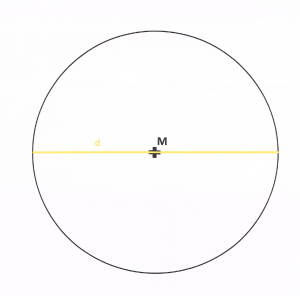
Der Durchmesser ist die Länge der Strecke zwischen zwei Punkten auf der Kreislinie, die durch den Mittelpunkt M verläuft. Der Durchmesser wird immer mit dem Kleinbuchstaben d bezeichnet. Für den Durchmesser gilt: Verdoppelst du den Radius r, so erhälst du den Durchmesser d, also: d = 2r
Beispiele aus dem Alltag
Kreise sind in unserem alltäglichen Leben oft anzutreffen. So besitzen folgende Dinge eine Kreisform:
- Uhr
- CD
- Schallplatte
Erzeugen und Zeichnen von Kreisen
Einen Kreis erzeugen
Ein Kreis lässt sich im Alltag auf vielfältige Arten erzeugen.
So entsteht ein Kreis beispielsweise, wenn man den Umriss eines zylinderförmigen Gegenstandes, durch Umfahren des Gegenstandes mit einem Stift, auf Papier festhält.
Einen Kreis zeichnen
Um einen Kreis zu zeichnen, brauchst du immer einen Zirkel. Mithilfe des Zirkels kannst du neben einem einfachen Kreis auch verschiedene Kreismuster anfertigen.
Weblinks
https://de.serlo.org/mathe/geometrie/dreiecke-vierecke-kreise-andere-ebene-figuren/kreise-kreisteile/kreis [26.01.2020]
Literatur
Franke, M. & Reinhold, S. (2016). Didaktik der Geometrie. In der Grundschule (3. Aufl.). Berlin: Springer Spektrum.