Haus der Vierecke: Unterschied zwischen den Versionen
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
:Ein symmetrisches Trapez ist ein Trapez, das [[achsensymmetrisch]] zur [[Mittelsenkrechte]]n der beiden parallelen Seiten ist. Da die [[Innenwinkel]] an den beiden parallelen Seiten gleich groß sind, wird es auch ''gleichschenkliges Trapez'' genannt. | :Ein symmetrisches Trapez ist ein Trapez, das [[achsensymmetrisch]] zur [[Mittelsenkrechte]]n der beiden parallelen Seiten ist. Da die [[Innenwinkel]] an den beiden parallelen Seiten gleich groß sind, wird es auch ''gleichschenkliges Trapez'' genannt. | ||
;Parallelogramm | ;Parallelogramm | ||
:Ein Parallelogramm ist ein Viereck, bei dem | :Ein Parallelogramm ist ein Viereck, bei dem beide sich gegenüberliegende Seitenpaare zueinander parallel sind. | ||
;Drachenviereck | ;Drachenviereck | ||
:Ein Drachenviereck ist ein Viereck, das zwei Paar gleich langer benachbarter Seiten besitzt und bei dem eine [[Diagonale]] die [[Symmetrieachse]] ist. | :Ein Drachenviereck ist ein Viereck, das zwei Paar gleich langer benachbarter Seiten besitzt und bei dem eine [[Diagonale]] die [[Symmetrieachse]] ist. | ||
| Zeile 22: | Zeile 22: | ||
=Aufbau= | =Aufbau= | ||
Je höher das Stockwerk ist, in dem sich ein Viereck befindet, desto mehr besondere Eigenschaften besitzt es. Das allgemeine Viereck ohne besondere Eigenschaften befindet sich dementsprechend ganz unten im Haus der Vierecke. Über ihm befindet sich das allgemeine Trapez, da es sich durch zwei zueinander parallele Seiten auszeichnet. Über dem allgemeinen Trapez befinden sich das Parallelogramm und das symmetrische Trapez. Das symmetrische Trapez zeichnet sich zusätzlich zu den zwei parallelen Seiten durch seine Achsensymmetrie aus, und beim Parallelogramm sind statt einem Seitenpaar gleich beide Seitenpaare parallel. Befindet sich ein Viereck über einem anderen Viereck, besitzt es also auch alle Eigenschaften des darunter liegenden Vierecks. So hat das Quadrat seinen Platz ganz oben im Dach und besitzt sowohl die Eigenschaften einer Raute als auch eines Rechtecks. Das Rechteck weist wiederum sowohl die Eigenschaften eines Parallelogramms und als auch eines symmetrischen Trapezes auf und befindet sich dementsprechend im Haus über | Je höher das Stockwerk ist, in dem sich ein Viereck befindet, desto mehr besondere Eigenschaften besitzt es. Das allgemeine Viereck ohne besondere Eigenschaften befindet sich dementsprechend ganz unten im Haus der Vierecke. Über ihm befindet sich das allgemeine Trapez, da es sich durch zwei zueinander parallele Seiten auszeichnet. Über dem allgemeinen Trapez befinden sich das Parallelogramm und das symmetrische Trapez. Das symmetrische Trapez zeichnet sich zusätzlich zu den zwei parallelen Seiten durch seine Achsensymmetrie aus, und beim Parallelogramm sind statt einem Seitenpaar gleich beide Seitenpaare parallel. Befindet sich ein Viereck über einem anderen Viereck, besitzt es also auch alle Eigenschaften des darunter liegenden Vierecks. So hat das Quadrat seinen Platz ganz oben im Dach und besitzt sowohl die Eigenschaften einer Raute als auch eines Rechtecks. Das Rechteck weist wiederum sowohl die Eigenschaften eines Parallelogramms und als auch eines symmetrischen Trapezes auf und befindet sich dementsprechend im Haus über beiden. | ||
=Beispielaussagen= | =Beispielaussagen= | ||
Aktuelle Version vom 5. Oktober 2020, 12:25 Uhr
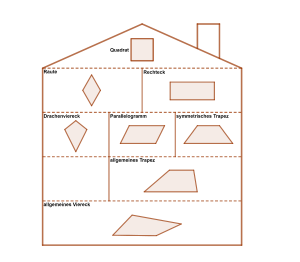
Das Haus der Vierecke veranschaulicht die Beziehungen zwischen den verschiedenen Vierecken, indem es diese hierarchisch nach ihren Eigenschaften ordnet.
Die Vierecke
Folgende Vierecke sind im Haus der Vierecke vertreten:
- Allgemeines Viereck
- Ein allgemeines Viereck ist ein Viereck ohne besondere Eigenschaften.
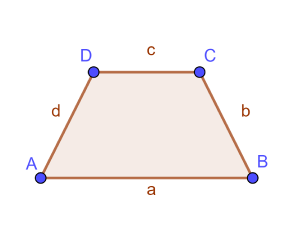
- Allgemeines Trapez
- Ein allgemeines Trapez ist ein Viereck mit zwei parallel zueinander liegenden Seiten.
- Symmetrisches Trapez
- Ein symmetrisches Trapez ist ein Trapez, das achsensymmetrisch zur Mittelsenkrechten der beiden parallelen Seiten ist. Da die Innenwinkel an den beiden parallelen Seiten gleich groß sind, wird es auch gleichschenkliges Trapez genannt.
- Parallelogramm
- Ein Parallelogramm ist ein Viereck, bei dem beide sich gegenüberliegende Seitenpaare zueinander parallel sind.
- Drachenviereck
- Ein Drachenviereck ist ein Viereck, das zwei Paar gleich langer benachbarter Seiten besitzt und bei dem eine Diagonale die Symmetrieachse ist.
- Raute
- Eine Raute (auch Rhombus) ist ein Viereck mit vier gleichlangen Seiten.
- Rechteck
- Ein Rechteck ist ein Viereck, bei dem alle Innenwinkel rechtwinklig sind.
- Quadrat
- Ein Quadrat ist ein Rechteck mit vier gleichlangen Seiten.
Aufbau
Je höher das Stockwerk ist, in dem sich ein Viereck befindet, desto mehr besondere Eigenschaften besitzt es. Das allgemeine Viereck ohne besondere Eigenschaften befindet sich dementsprechend ganz unten im Haus der Vierecke. Über ihm befindet sich das allgemeine Trapez, da es sich durch zwei zueinander parallele Seiten auszeichnet. Über dem allgemeinen Trapez befinden sich das Parallelogramm und das symmetrische Trapez. Das symmetrische Trapez zeichnet sich zusätzlich zu den zwei parallelen Seiten durch seine Achsensymmetrie aus, und beim Parallelogramm sind statt einem Seitenpaar gleich beide Seitenpaare parallel. Befindet sich ein Viereck über einem anderen Viereck, besitzt es also auch alle Eigenschaften des darunter liegenden Vierecks. So hat das Quadrat seinen Platz ganz oben im Dach und besitzt sowohl die Eigenschaften einer Raute als auch eines Rechtecks. Das Rechteck weist wiederum sowohl die Eigenschaften eines Parallelogramms und als auch eines symmetrischen Trapezes auf und befindet sich dementsprechend im Haus über beiden.
Beispielaussagen
Folgende beispielhafte Aussagen lassen sich leicht mit dem Haus der Vierecke ableiten:
- Jedes Parallelogramm ist ein (allgemeines) Trapez.
- Jedes Rechteck ist ein Parallelogramm.
- Jedes Quadrat ist ein Drachenviereck.
- Jede Raute ist ein Parallelogramm.
- Jedes Quadrat ist eine Raute.
Übungsaufgabe
Begründe, warum sich das Drachenviereck im Haus der Vierecke unter der Raute befindet!