Mittelsenkrechte: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (9 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Die Mittelsenkrechte ist eine | Die Mittelsenkrechte ist eine [[Geraden]], die senkrecht zu einer [[Strecken]] (oder Geraden) und durch einen Mittelpunkt M dieser Strecke (oder Geraden) verläuft. Sie ist eine der besonderen [[Linien im Dreieck]]. | ||
=Definition= | =Definition= | ||
[[Datei:Mittelsenkrechte allg.jpg|200px|thumb|right|Mittelsenkrechte (rot) zur Strecke AB.]] | [[Datei:Mittelsenkrechte allg.jpg|200px|thumb|right|Mittelsenkrechte (rot) zur Strecke AB.]] | ||
Es ist eine Strecke AB und ihr Mittelpunkt M gegeben. Die Mittelsenkrechte ist eine Gerade, die durch den Punkt M verläuft und senkrecht zur Strecke steht. | Es ist eine Strecke AB und ihr Mittelpunkt M gegeben. Die Mittelsenkrechte ist eine Gerade, die durch den Punkt M verläuft und senkrecht zur Strecke steht. | ||
=Eigenschaften= | =Eigenschaften= | ||
[[Datei:Mittelsenkrechte Eigenschaft.jpg|200px|thumb|left|Darstellung der Eigenschaft]] Jeder Punkt P, der auf der Mittelsenkrechten liegt, ist gleichweit entfernt von den Eckpunkten A und B der Strecke. Anders herum gilt: Jeder Punkt Q, der nicht auf der Mittelsenkrechten liegt, hat eine unterschiedliche Entfernung zu den Eckpunkten A und B. | [[Datei:Mittelsenkrechte Eigenschaft.jpg|200px|thumb|left|Darstellung der Eigenschaft]] Jeder Punkt P, der auf der Mittelsenkrechten liegt, ist gleichweit entfernt von den Eckpunkten A und B der Strecke. Anders herum gilt: Jeder Punkt Q, der nicht auf der Mittelsenkrechten liegt, hat eine unterschiedliche Entfernung zu den Eckpunkten A und B. | ||
==Mittelsenkrechte im Dreieck== | ==Mittelsenkrechte im Dreieck== | ||
| Zeile 16: | Zeile 14: | ||
=Konstruktion= | =Konstruktion= | ||
==Mit einem Geodreieck oder Winkelmesser== | ==Mit einem Geodreieck oder Winkelmesser== | ||
Um die Mittelsenkrechte zu konstruieren, wird im 90° Winkel zur Strecke | Um die Mittelsenkrechte zu konstruieren, wird im 90° Winkel zur Strecke AB eine Gerade durch den Punkt M gezeichnet. | ||
==Mit dem Zirkel== | ==Mit dem Zirkel== | ||
Um die Mittelsenkrechte mit dem Zirkel zu zeichnen, nutzt man die Eigenschaft, dass alle Punkte der Mittelsenkrechten gleichweit entfernt zu den Eckpunkten liegen. Man spannt im Zirkel einen Radius ein, der länger als die Hälfte der Strecke ist. Nun zeichnet man jeweils einen Kreis um die Eckpunkte A und B. Es ergeben sich 2 Schnittpunkte. Die Gerade durch die beiden Schnittpunkte ist die Mittelsenkrechte. Um genau zu zeichnen kann man auch mehrere Kreise jeweils um die Eckpunkte A und B zeichnen, sodass sich mehrere Schnittpunkte ergeben. Wichtig dabei ist, dass der Radius stets größer als die Hälfte der Strecke | [[Datei:Mittelsenkrechte KonstruktionZirkel.jpg|mini|Konstruktion der Mittelsenkrechten (rot) der Strecke AB]] | ||
Um die Mittelsenkrechte mit dem Zirkel zu zeichnen, nutzt man die Eigenschaft, dass alle Punkte der Mittelsenkrechten gleichweit entfernt zu den Eckpunkten liegen. Man spannt im Zirkel einen Radius ein, der länger als die Hälfte der Strecke ist. Nun zeichnet man jeweils einen Kreis um die Eckpunkte A und B. Es ergeben sich 2 Schnittpunkte der [[Kreise]]. Die Gerade durch die beiden Schnittpunkte ist die Mittelsenkrechte. Um genau zu zeichnen kann man auch mehrere Kreise jeweils um die Eckpunkte A und B zeichnen, sodass sich mehrere Schnittpunkte ergeben. Wichtig dabei ist, dass der Radius stets größer als die Hälfte der Strecke AB ist. | |||
=Übungsaufgabe= | |||
Zeichne das Dreieck ABC in ein Koordinatensystem mit der Einheit 1cm. Konstruiere den Umkreis und bestimme den näherungsweise den Mittelpunkt. Nutze dafür | |||
*(a) Geodreieck oder Winkelmesser. | |||
*(b) Zirkel. | |||
1.) A(1|3) B(10|4) C(6|8) | |||
2.) A(5|1) B(10|9) C(2|8) | |||
=Lösung= | |||
Bei der ersten Aufgabe hat der Mittelpunkt hat einen Abstand von etwa Drei Komma Fünf Zentimetern in Y-Richtung und etwa Fünf Komma Fünf Zentimetern in X-Richtung. Bei der zweiten Aufgabe hat der Schnittpunkt der Mittelsenkrechten einen Abstand von etwa Sechs Komma Vier Zentimetern in X-Richtung und etwa Fünf Komma Sieben Zentimeter in Y-Richtung. | |||
[[Kategorie:Geometrie]] | |||
Aktuelle Version vom 26. September 2020, 10:41 Uhr
Die Mittelsenkrechte ist eine Geraden, die senkrecht zu einer Strecken (oder Geraden) und durch einen Mittelpunkt M dieser Strecke (oder Geraden) verläuft. Sie ist eine der besonderen Linien im Dreieck.
Definition
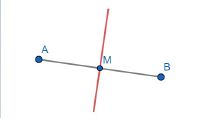
Es ist eine Strecke AB und ihr Mittelpunkt M gegeben. Die Mittelsenkrechte ist eine Gerade, die durch den Punkt M verläuft und senkrecht zur Strecke steht.
Eigenschaften
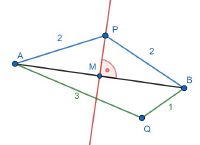
Jeder Punkt P, der auf der Mittelsenkrechten liegt, ist gleichweit entfernt von den Eckpunkten A und B der Strecke. Anders herum gilt: Jeder Punkt Q, der nicht auf der Mittelsenkrechten liegt, hat eine unterschiedliche Entfernung zu den Eckpunkten A und B.
Mittelsenkrechte im Dreieck
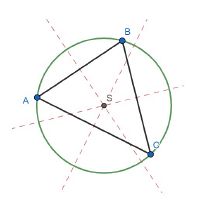
Alle drei Mittelsenkrechten eines Dreiecks schneiden sich in genau einem Punkt S. Dieser Punkt ist der Mittelpunkt des Umkreises. Er schneidet alle drei Ecken des Dreiecks.
Konstruktion
Mit einem Geodreieck oder Winkelmesser
Um die Mittelsenkrechte zu konstruieren, wird im 90° Winkel zur Strecke AB eine Gerade durch den Punkt M gezeichnet.
Mit dem Zirkel
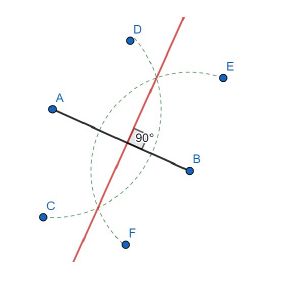
Um die Mittelsenkrechte mit dem Zirkel zu zeichnen, nutzt man die Eigenschaft, dass alle Punkte der Mittelsenkrechten gleichweit entfernt zu den Eckpunkten liegen. Man spannt im Zirkel einen Radius ein, der länger als die Hälfte der Strecke ist. Nun zeichnet man jeweils einen Kreis um die Eckpunkte A und B. Es ergeben sich 2 Schnittpunkte der Kreise. Die Gerade durch die beiden Schnittpunkte ist die Mittelsenkrechte. Um genau zu zeichnen kann man auch mehrere Kreise jeweils um die Eckpunkte A und B zeichnen, sodass sich mehrere Schnittpunkte ergeben. Wichtig dabei ist, dass der Radius stets größer als die Hälfte der Strecke AB ist.
Übungsaufgabe
Zeichne das Dreieck ABC in ein Koordinatensystem mit der Einheit 1cm. Konstruiere den Umkreis und bestimme den näherungsweise den Mittelpunkt. Nutze dafür
- (a) Geodreieck oder Winkelmesser.
- (b) Zirkel.
1.) A(1|3) B(10|4) C(6|8)
2.) A(5|1) B(10|9) C(2|8)
Lösung
Bei der ersten Aufgabe hat der Mittelpunkt hat einen Abstand von etwa Drei Komma Fünf Zentimetern in Y-Richtung und etwa Fünf Komma Fünf Zentimetern in X-Richtung. Bei der zweiten Aufgabe hat der Schnittpunkt der Mittelsenkrechten einen Abstand von etwa Sechs Komma Vier Zentimetern in X-Richtung und etwa Fünf Komma Sieben Zentimeter in Y-Richtung.