Winkelhalbierende: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „Kategorie: Geometrie Die Winkelhalbierende ist eine Halbgerade, die durch den Scheitel eines Winkels verläuft und diesen in zwei gleichgroße Wi…“ |
Keine Bearbeitungszusammenfassung |
||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Kategorie: Geometrie]] | [[Kategorie: Geometrie]] | ||
Die Winkelhalbierende ist eine [[Halbgerade]], die durch den Scheitel eines [[Winkels]] verläuft und diesen in zwei gleichgroße [[Winkelfelder]] teilt. Sie ist wie die [[Mittelsenkrechte]] eine der besonderen [[Linien im Dreieck]]. | |||
Die Winkelhalbierende ist eine [[Halbgerade]], die durch den [[Scheitel]] eines [[Winkels]] verläuft und diesen in zwei gleichgroße [[Winkelfelder]] teilt. Sie ist wie die [[Mittelsenkrechte]] eine der besonderen [[Linien im Dreieck]]. | |||
=Definition= | =Definition= | ||
Die Winkelhalbierende ist eine Halbgerade < | [[Datei: Def.png|200px|thumb|right|Veranschaulichung der Definition.]] | ||
Die Winkelhalbierende ist eine Halbgerade w_γ, die durch den Scheitel S eines Winkels γ verläuft und dabei das zugehörige Winkelfeld halbiert. <ref>vgl. Scheid, H.; Schwarz, W. (2007). Elemente der Geometrie. 4. Auflage. München: Spektrum Akademischer Verlag. S. 11</ref> | |||
=Eigenschaften= | =Eigenschaften= | ||
==Punkte auf der Winkelhalbierenden== | |||
[[Datei:Abstand.png|200px|thumb|right]] | |||
Für alle Punkte P, die auf der Winkelhalbierenden liegen, gilt, dass der [[Abstand]] von den beiden [[Schenkeln]] gleichgroß ist. Es gilt also unter Verwendung der nebenstehenden Skizze, dass die beiden [[Strecken]] a und b gleichlang sind. <ref>vgl. Scheid, H.; Schwarz, W. (2007). Elemente der Geometrie. 4. Auflage. München: Spektrum Akademischer Verlag. S. 11</ref> | |||
==Schneidende Geradenpaare== | ==Schneidende Geradenpaare== | ||
[[Datei:Schneiden.png|200px|thumb|left]] | |||
Wenn sich zwei [[Geraden]] g und h schneiden, entstehen am Schnittpunkt, welcher als Scheitelpunkt fungiert, vier Winkel. Dabei lässt sich jedem Winkel genau zwei [[Nebenwinkel]] und genau einen [[Gegenwinkel]] zuordnen. Werden die Winkelhalbierenden eines Winkels α und eines beliebigen zugehörigen Nebenwinkels β gebildet, so stehen diese Halbgeraden [[senkrecht]] aufeinander. Es gilt: w_α ⊥w_β. <ref>vgl. Scheid, H.; Schwarz, W. (2007). Elemente der Geometrie. 4. Auflage. München: Spektrum Akademischer Verlag. S. 11</ref> | |||
==Winkelhalbierende im Dreieck== | ==Winkelhalbierende im Dreieck== | ||
[[Datei:Inkreis.png|200px|right|left]] | |||
Die Winkelhalbierenden der [[Innenwinkel]] eines Dreiecks ΔABC schneiden sich in einem Punkt M. Dieser ist Mittelpunkt eines [[Kreises]], der die drei Seiten berührt und somit in das Dreieck einbeschrieben ist. Der besondere Kreis wird [[Inkreis]] des Dreiecks genannt, der zugehörige Mittelpunkt Inkreismittelpunkt M. <ref>vgl. Scheid, H.; Schwarz, W. (2007). Elemente der Geometrie. 4. Auflage. München: Spektrum Akademischer Verlag. S. 20</ref> | |||
| Zeile 19: | Zeile 50: | ||
=Konstruktion= | =Konstruktion= | ||
[[Datei:Konstruktion.png|300px|thumb|right|Darstellung der Hilfslinien und des fertigen Konstruktionsbildes.]] | |||
Die Winkelhalbierende kann mithilfe eines Lineals und eines Zirkels konstruiert werden. Zunächst wird mit dem Zirkel ein Kreis mit dem Scheitel des Winkels als Mittelpunkt gezeichnet. Dabei ist es ausreichend, die Schnittpunkte der [[Kreislinie]] mit den beiden Schenkeln einzuzeichnen. Anschließend werden zwei weitere Kreise mit gleichem, hinreichend großem [[Radius]] so konstruiert, dass die Mittelpunkte die Schnittpunkte des ersten Kreises mit den Schenkeln darstellen. Hier ist wiederum nur einer der Schnittpunkte der beiden Kreislinien relevant, sodass dessen Kennzeichnung ausreicht. Abschließend wird der erhaltene Schnittpunkt mit dem Scheitel des Winkels zu einer Halbgeraden verbunden. <ref>vgl. Hajós, G. (1970). Einführung in die Geometrie. Leipzig: BSB B. G. Teubner Verlagsgesellschaft. S. 195-196</ref> | |||
= | |||
=Beispielaufgabe= | |||
Im Folgenden soll eine Aufgabe zur Anwendung der Konstruktion von Winkelhalbierenden im Dreieck dargestellt werden. | |||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Zeichne das Dreieck ΔABC mit den vorgegebenen Punkten in ein Koordinatensystem und bestimme den Radius des zugehörigen Inkreises. | |||
A=(0;0), B=(4;1), C=(2;5) | |||
==Lösung== | ==Lösung== | ||
[[Datei:BspAfg.png|300px|thumb|left]] | |||
Die nebenstehende Abbildung zeigt die Lösung der Aufgabenstellung. Der Radius des Inkreises beträgt etwa 1,3 Längeneinheiten. | |||
=Referenzen= | |||
Aktuelle Version vom 26. September 2020, 17:18 Uhr
Die Winkelhalbierende ist eine Halbgerade, die durch den Scheitel eines Winkels verläuft und diesen in zwei gleichgroße Winkelfelder teilt. Sie ist wie die Mittelsenkrechte eine der besonderen Linien im Dreieck.
Definition
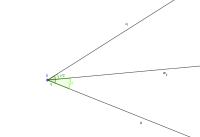
Die Winkelhalbierende ist eine Halbgerade w_γ, die durch den Scheitel S eines Winkels γ verläuft und dabei das zugehörige Winkelfeld halbiert. [1]
Eigenschaften
Punkte auf der Winkelhalbierenden
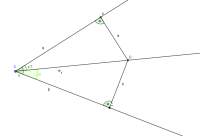
Für alle Punkte P, die auf der Winkelhalbierenden liegen, gilt, dass der Abstand von den beiden Schenkeln gleichgroß ist. Es gilt also unter Verwendung der nebenstehenden Skizze, dass die beiden Strecken a und b gleichlang sind. [2]
Schneidende Geradenpaare
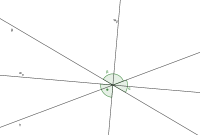
Wenn sich zwei Geraden g und h schneiden, entstehen am Schnittpunkt, welcher als Scheitelpunkt fungiert, vier Winkel. Dabei lässt sich jedem Winkel genau zwei Nebenwinkel und genau einen Gegenwinkel zuordnen. Werden die Winkelhalbierenden eines Winkels α und eines beliebigen zugehörigen Nebenwinkels β gebildet, so stehen diese Halbgeraden senkrecht aufeinander. Es gilt: w_α ⊥w_β. [3]
Winkelhalbierende im Dreieck
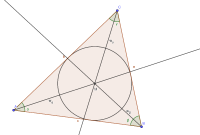
Die Winkelhalbierenden der Innenwinkel eines Dreiecks ΔABC schneiden sich in einem Punkt M. Dieser ist Mittelpunkt eines Kreises, der die drei Seiten berührt und somit in das Dreieck einbeschrieben ist. Der besondere Kreis wird Inkreis des Dreiecks genannt, der zugehörige Mittelpunkt Inkreismittelpunkt M. [4]
Konstruktion
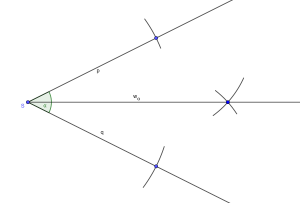
Die Winkelhalbierende kann mithilfe eines Lineals und eines Zirkels konstruiert werden. Zunächst wird mit dem Zirkel ein Kreis mit dem Scheitel des Winkels als Mittelpunkt gezeichnet. Dabei ist es ausreichend, die Schnittpunkte der Kreislinie mit den beiden Schenkeln einzuzeichnen. Anschließend werden zwei weitere Kreise mit gleichem, hinreichend großem Radius so konstruiert, dass die Mittelpunkte die Schnittpunkte des ersten Kreises mit den Schenkeln darstellen. Hier ist wiederum nur einer der Schnittpunkte der beiden Kreislinien relevant, sodass dessen Kennzeichnung ausreicht. Abschließend wird der erhaltene Schnittpunkt mit dem Scheitel des Winkels zu einer Halbgeraden verbunden. [5]
Beispielaufgabe
Im Folgenden soll eine Aufgabe zur Anwendung der Konstruktion von Winkelhalbierenden im Dreieck dargestellt werden.
Aufgabenstellung
Zeichne das Dreieck ΔABC mit den vorgegebenen Punkten in ein Koordinatensystem und bestimme den Radius des zugehörigen Inkreises.
A=(0;0), B=(4;1), C=(2;5)
Lösung
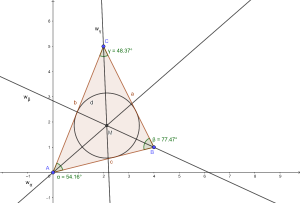
Die nebenstehende Abbildung zeigt die Lösung der Aufgabenstellung. Der Radius des Inkreises beträgt etwa 1,3 Längeneinheiten.
Referenzen
- ↑ vgl. Scheid, H.; Schwarz, W. (2007). Elemente der Geometrie. 4. Auflage. München: Spektrum Akademischer Verlag. S. 11
- ↑ vgl. Scheid, H.; Schwarz, W. (2007). Elemente der Geometrie. 4. Auflage. München: Spektrum Akademischer Verlag. S. 11
- ↑ vgl. Scheid, H.; Schwarz, W. (2007). Elemente der Geometrie. 4. Auflage. München: Spektrum Akademischer Verlag. S. 11
- ↑ vgl. Scheid, H.; Schwarz, W. (2007). Elemente der Geometrie. 4. Auflage. München: Spektrum Akademischer Verlag. S. 20
- ↑ vgl. Hajós, G. (1970). Einführung in die Geometrie. Leipzig: BSB B. G. Teubner Verlagsgesellschaft. S. 195-196