Zahlenketten: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „Kategorie: Zahlenkette '''Was sind Zahlenketten?''' Wir kennen bereits aus der Schule jede Menge Zahlen von 0 bis unendlich. Auch eine Kette, wie zum B…“ |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Kategorie: Zahlenkette]] | [[Kategorie: Zahlenkette]] | ||
Zahlenketten bestehen aus einzelnen [[Kettengliedern]]. Durch die [[Addition]] der vorherigen zwei Kettenglieder erhält man die [[Summe]] und somit das dritte Kettenglied. Dieses Vorgehen kann beliebig oft wiederholt werden. | |||
= Beispiel = | |||
Wir kennen bereits aus der Schule jede Menge Zahlen von 0 bis unendlich. Auch eine Kette, wie zum Beispiel eine Halskette oder Schneekette kommt uns bekannt vor. | Wir kennen bereits aus der Schule jede Menge [[Zahlen]] von [[0]] bis [[unendlich]]. Auch eine Kette, wie zum Beispiel eine Halskette oder Schneekette kommt uns bekannt vor. | ||
'''Aber wie genau könnten Zahlenketten in der Mathematik aussehen?''' | |||
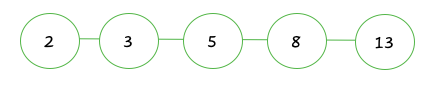
[[Datei:Beispiel_Zahlenkette.png]] | [[Datei:Beispiel_Zahlenkette.png]] | ||
= Vorgehen = | |||
Zahlenketten werden durch die [[Addition]] der Kettenelemente gebildet. Man beginnt mit zwei verschiedenen Startzahlen. Das dritte Kettenglied erhält man durch die Addition der beiden Startzahlen. Das Ergebnis der weiteren Kettenelemente erhält man immer wieder, indem man die beiden vorherigen Kettenelemente addiert. Das Prinzip sieht dem Rechnen mit den Zahlenmauern ganz ähnlich. Kannst du dich daran erinnern? Wenn du es noch nicht ganz verstanden hast, schau dir doch einfach das Video an. | Zahlenketten werden durch die [[Addition]] der [[Kettenelemente]] gebildet. Man beginnt mit zwei verschiedenen Startzahlen. Das dritte Kettenglied erhält man durch die [[Addition]]der beiden Startzahlen. Das Ergebnis der weiteren Kettenelemente erhält man immer wieder, indem man die beiden vorherigen Kettenelemente addiert. Das Prinzip sieht dem Rechnen mit den [[Zahlenmauern]] ganz ähnlich. Kannst du dich daran erinnern? Wenn du es noch nicht ganz verstanden hast, schau dir doch einfach das Video an. | ||
[https://pikas.dzlm.de/node/1315] | [https://pikas.dzlm.de/node/1315] | ||
| Zeile 19: | Zeile 20: | ||
---- | ---- | ||
''Rechne doch selber mal:'' | = Rechnung = | ||
''' Rechne doch selber mal: ''' | |||
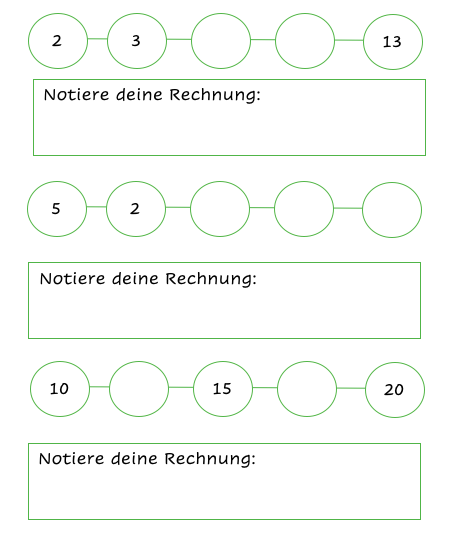
[[Datei:Aufgaben_Zahlenkette.png]] | [[Datei:Aufgaben_Zahlenkette.png]] | ||
| Zeile 25: | Zeile 28: | ||
---- | ---- | ||
= Mathematische Struktur = | |||
'''Welche mathematische Grundstruktur steckt dahinter?''' | ''' Welche mathematische Grundstruktur steckt dahinter? ''' | ||
Die algebraische Darstellung soll noch einmal die Grundstruktur darstellen. | Die [[algebraische]] Darstellung soll noch einmal die Grundstruktur darstellen. | ||
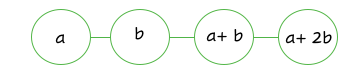
[[Datei:Algebraische_Struktur.png]] | [[Datei:Algebraische_Struktur.png]] | ||
Zahlenketten mit der abgebildeteten Grundstruktur können bereits in der ersten Klasse eingesetzt werden, sofern die Kettenglieder begrenzt werden. Das Erkennen von mathematischen Strukturen, Mustern und Zusammenhänge soll bereits früh geübt werden. Beim Rechnen werden die Kinder automatisch in höheren Zahlenräumen als vorgesehen rechnen, was einen Anreiz schafft mit größeren Zahlen zu rechnen und nicht als problematisch angesehen werden muss. | Zahlenketten mit der abgebildeteten Grundstruktur können bereits in der ersten Klasse eingesetzt werden, sofern die [[Kettenglieder]] begrenzt werden. Das Erkennen von mathematischen Strukturen, Mustern und Zusammenhänge soll bereits früh geübt werden. Beim Rechnen werden die Kinder automatisch in höheren Zahlenräumen als vorgesehen rechnen, was einen Anreiz schafft mit größeren Zahlen zu rechnen und nicht als problematisch angesehen werden muss. | ||
Vor allem für rechenstarke Schüler*innen bieten die Zahlenketten einen unglaublichen Differenzierungsspielraum. Es können beliebige Kettenelemente weggelassen werden, alle Elemte frei gelassen werden oder nur das letzte Element eingetragen sein. | Vor allem für rechenstarke Schüler*innen bieten die Zahlenketten einen unglaublichen Differenzierungsspielraum. Es können beliebige Kettenelemente weggelassen werden, alle Elemte frei gelassen werden oder nur das letzte Element eingetragen sein. | ||
| Zeile 42: | Zeile 46: | ||
---- | ---- | ||
= Quellen = | |||
Landesinstitut für Schulentwicklung (2021). Zahlenketten. [https://www.schule-bw.de/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/grundschule/sinus-grundschule/gute-aufgaben/docs/Zahlenketten.pdf] | Landesinstitut für Schulentwicklung (2021). Zahlenketten. [https://www.schule-bw.de/faecher-und-schularten/mathematisch-naturwissenschaftliche-faecher/mathematik/unterrichtsmaterialien/grundschule/sinus-grundschule/gute-aufgaben/docs/Zahlenketten.pdf] | ||
Deutsches Zentrum für Lehrerbildung Mathematik (2021). Pikas. [https://pikas.dzlm.de/material-pik/mathematische-bildung/haus-1-unterrichts-material/unterrichtsreihe-zahlenketten] | Deutsches Zentrum für Lehrerbildung Mathematik (2021). Pikas. [https://pikas.dzlm.de/material-pik/mathematische-bildung/haus-1-unterrichts-material/unterrichtsreihe-zahlenketten] | ||
Aktuelle Version vom 4. März 2021, 08:57 Uhr
Zahlenketten bestehen aus einzelnen Kettengliedern. Durch die Addition der vorherigen zwei Kettenglieder erhält man die Summe und somit das dritte Kettenglied. Dieses Vorgehen kann beliebig oft wiederholt werden.
Beispiel
Wir kennen bereits aus der Schule jede Menge Zahlen von 0 bis unendlich. Auch eine Kette, wie zum Beispiel eine Halskette oder Schneekette kommt uns bekannt vor.
Aber wie genau könnten Zahlenketten in der Mathematik aussehen?
Vorgehen
Zahlenketten werden durch die Addition der Kettenelemente gebildet. Man beginnt mit zwei verschiedenen Startzahlen. Das dritte Kettenglied erhält man durch die Additionder beiden Startzahlen. Das Ergebnis der weiteren Kettenelemente erhält man immer wieder, indem man die beiden vorherigen Kettenelemente addiert. Das Prinzip sieht dem Rechnen mit den Zahlenmauern ganz ähnlich. Kannst du dich daran erinnern? Wenn du es noch nicht ganz verstanden hast, schau dir doch einfach das Video an. [1]
Rechnung
Rechne doch selber mal:
Mathematische Struktur
Welche mathematische Grundstruktur steckt dahinter?
Die algebraische Darstellung soll noch einmal die Grundstruktur darstellen.
Zahlenketten mit der abgebildeteten Grundstruktur können bereits in der ersten Klasse eingesetzt werden, sofern die Kettenglieder begrenzt werden. Das Erkennen von mathematischen Strukturen, Mustern und Zusammenhänge soll bereits früh geübt werden. Beim Rechnen werden die Kinder automatisch in höheren Zahlenräumen als vorgesehen rechnen, was einen Anreiz schafft mit größeren Zahlen zu rechnen und nicht als problematisch angesehen werden muss. Vor allem für rechenstarke Schüler*innen bieten die Zahlenketten einen unglaublichen Differenzierungsspielraum. Es können beliebige Kettenelemente weggelassen werden, alle Elemte frei gelassen werden oder nur das letzte Element eingetragen sein.
Quellen
Landesinstitut für Schulentwicklung (2021). Zahlenketten. [2]
Deutsches Zentrum für Lehrerbildung Mathematik (2021). Pikas. [3]