Dreieck: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „Das Dreieck ist die einfachste ebene Figur. Es besteht aus drei Seiten, drei Ecken und drei Winkeln. Die Summe aller inneren Winkel (Innenwinkel) beträgt 180…“ |
Keine Bearbeitungszusammenfassung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Das Dreieck ist die einfachste ebene Figur. Es besteht aus drei Seiten, drei Ecken und drei | Das Dreieck ist die einfachste [[ebene Figur]]. Es besteht aus drei Seiten, drei Ecken und drei [[Winkel]]n. Die Summe aller inneren Winkel ([[Innenwinkel]]) beträgt 180°. | ||
== Arten von Dreiecken == | == Arten von Dreiecken == | ||
[[Datei:Allgemeines Dreieck.PNG|thumb|Allgemeines Dreieck]] | [[Datei:Allgemeines Dreieck.PNG|thumb|Allgemeines Dreieck]] | ||
Dreiecke können unterschiedlich lange Seiten, oder unterschiedlich große Winkel besitzen. Je nach Seitenlänge oder Winkelgröße lassen sich die Dreiecke in Kategorien einordnen. | Dreiecke können unterschiedlich lange Seiten, oder unterschiedlich große Winkel besitzen. Je nach Seitenlänge oder Winkelgröße lassen sich die Dreiecke in Kategorien einordnen. Manchen Dreiecken können auch mehrere Merkmale zugeschrieben werden. Betrachtet man die Seitenlängen, so sind diese Eigenschaften: | ||
:* '''gleichseitig''': alle Seiten des Dreiecks sind gleich lang | :* '''gleichseitig''': alle Seiten des Dreiecks sind gleich lang | ||
:* '''ungleichseitig''': alle Seiten des Dreiecks sind unterschiedlich lang | :* '''ungleichseitig''': alle Seiten des Dreiecks sind unterschiedlich lang | ||
:* '''gleichschenklig''': mindestens zwei Seiten des Dreiecks sind gleich lang | :* '''gleichschenklig''': mindestens zwei Seiten des Dreiecks sind gleich lang | ||
Betrachtet man die Winkel, so ergeben sich diese Eigenschaften: | Betrachtet man die Winkel, so ergeben sich diese Eigenschaften: | ||
:* '''rechtwinklig''': ein Winkels des Dreiecks ist ein rechter Winkel (90°) | :* '''rechtwinklig''': ein Winkels des Dreiecks ist ein [[rechter Winkel]] (90°) | ||
:* '''spitzwinklig''': alle Winkel des Dreiecks sind spitze Winkel (<90°) | :* '''spitzwinklig''': alle Winkel des Dreiecks sind spitze Winkel (<90°) | ||
:* '''stumpfwinklig''': ein Winkel des Dreiecks ist ein stumpfer Winkel (zwischen 90° und 180°) | :* '''stumpfwinklig''': ein Winkel des Dreiecks ist ein stumpfer Winkel (zwischen 90° und 180°) | ||
== Beschriftung des Dreiecks == | == Beschriftung des Dreiecks == | ||
[[Datei: | |||
[[Datei:Dreieck Beschriftung.PNG|thumb|Dreieck mit Beschriftung]] | |||
Dreiecke werden mit Buchstaben beschriftet. Für die Eckpunkte werden große Buchstaben verwendet. Die Beschriftung erfolgt meistens mit den ersten Buchstaben des [[Alphabet]]s, also '''A''', '''B''' und '''C'''. Die Seiten werden mit kleinen Buchstaben beschriftet. Dabei erhält die Seite, die dem Punkt A gegenüberliegt den kleinen Buchstaben '''a'''. Genau so verhält es sich für die gegenüberliegenden Seiten zu den Punkten B und C. Diese werden mit '''b''' und '''c''' beschriftet Die Winkel werden mit griechischen Buchstaben beschriftet. Die ersten drei Buchstaben lauten '''Alpha (α)''', '''Beta (β)''' und '''Gamma (γ)'''. | |||
== Berechnungen am Dreieck == | |||
=== Umfang === | |||
Um den [[Umfang]] eines Dreiecks zu berechnen, addiert man alle Seitenlängen des Dreiecks miteinander. U = a + b + c | |||
=== Flächeninhalt === | |||
[[Datei:Flächeninhalt_Dreieck.PNG|thumb|Dreieck mit eingezeichneter Höhe]] | |||
Der [[Flächeninhalt]] des Dreiecks lässt sich mit der [[Höhe]] des Dreiecks ausrechnen. Die Höhe steht [[senkrecht]] auf der '''Grundseite''' des Dreiecks. Sie erstreckt sich bis zum gegenüberliegenden Eckpunkt Bei dem Dreieck auf dem Beispiel rechts ist die Grundseite die Seite a und der gegenüberliegende Eckpunkt ist A. Die Formel für den Flächeninhalt lautet A = ½ ∙ a ∙ h | |||
=== Übungsaufgaben === | |||
:* Wie ist der Umfang eines Dreiecks mit den Seitenlängen a = 6cm, b = 4cm, c = 5cm? | |||
:* Welchen Flächeninhalt hat ein Dreieck mit a = 7cm und h = 5cm? | |||
:* Wie nennt man ein Dreieck mit den Innenwinkeln α = 78°, β = 90° und γ = 12°? | |||
Aktuelle Version vom 2. April 2021, 16:36 Uhr
Das Dreieck ist die einfachste ebene Figur. Es besteht aus drei Seiten, drei Ecken und drei Winkeln. Die Summe aller inneren Winkel (Innenwinkel) beträgt 180°.
Arten von Dreiecken
Dreiecke können unterschiedlich lange Seiten, oder unterschiedlich große Winkel besitzen. Je nach Seitenlänge oder Winkelgröße lassen sich die Dreiecke in Kategorien einordnen. Manchen Dreiecken können auch mehrere Merkmale zugeschrieben werden. Betrachtet man die Seitenlängen, so sind diese Eigenschaften:
- gleichseitig: alle Seiten des Dreiecks sind gleich lang
- ungleichseitig: alle Seiten des Dreiecks sind unterschiedlich lang
- gleichschenklig: mindestens zwei Seiten des Dreiecks sind gleich lang
Betrachtet man die Winkel, so ergeben sich diese Eigenschaften:
- rechtwinklig: ein Winkels des Dreiecks ist ein rechter Winkel (90°)
- spitzwinklig: alle Winkel des Dreiecks sind spitze Winkel (<90°)
- stumpfwinklig: ein Winkel des Dreiecks ist ein stumpfer Winkel (zwischen 90° und 180°)
Beschriftung des Dreiecks
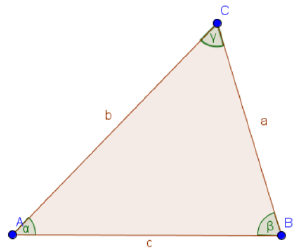
Dreiecke werden mit Buchstaben beschriftet. Für die Eckpunkte werden große Buchstaben verwendet. Die Beschriftung erfolgt meistens mit den ersten Buchstaben des Alphabets, also A, B und C. Die Seiten werden mit kleinen Buchstaben beschriftet. Dabei erhält die Seite, die dem Punkt A gegenüberliegt den kleinen Buchstaben a. Genau so verhält es sich für die gegenüberliegenden Seiten zu den Punkten B und C. Diese werden mit b und c beschriftet Die Winkel werden mit griechischen Buchstaben beschriftet. Die ersten drei Buchstaben lauten Alpha (α), Beta (β) und Gamma (γ).
Berechnungen am Dreieck
Umfang
Um den Umfang eines Dreiecks zu berechnen, addiert man alle Seitenlängen des Dreiecks miteinander. U = a + b + c
Flächeninhalt
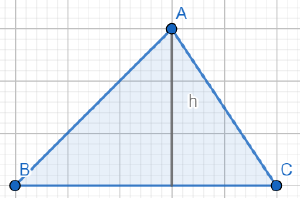
Der Flächeninhalt des Dreiecks lässt sich mit der Höhe des Dreiecks ausrechnen. Die Höhe steht senkrecht auf der Grundseite des Dreiecks. Sie erstreckt sich bis zum gegenüberliegenden Eckpunkt Bei dem Dreieck auf dem Beispiel rechts ist die Grundseite die Seite a und der gegenüberliegende Eckpunkt ist A. Die Formel für den Flächeninhalt lautet A = ½ ∙ a ∙ h
Übungsaufgaben
- Wie ist der Umfang eines Dreiecks mit den Seitenlängen a = 6cm, b = 4cm, c = 5cm?
- Welchen Flächeninhalt hat ein Dreieck mit a = 7cm und h = 5cm?
- Wie nennt man ein Dreieck mit den Innenwinkeln α = 78°, β = 90° und γ = 12°?