Peripherie – Zentriwinkel – Satz: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Die Seite wurde neu angelegt: „ kurze Einleitung = Erkärung = Die über einem Bogen und einer Sehne liegenden '''Peripheriewinkel''' eines Kreises sind untereinander gleich und halb so gr…“ |
Keine Bearbeitungszusammenfassung |
||
| Zeile 5: | Zeile 5: | ||
= Erkärung = | = Erkärung = | ||
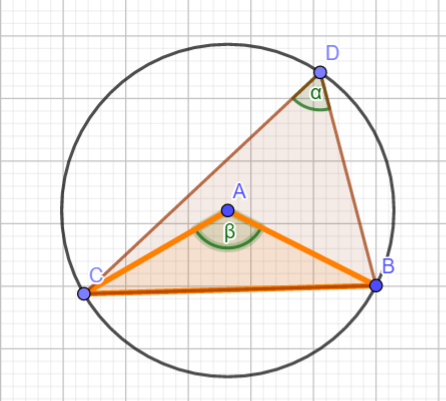
Die über einem Bogen und einer Sehne liegenden '''Peripheriewinkel''' eines Kreises sind untereinander gleich und halb so groß wie der zugehörige '''Zentriwinkel'''. | Die über einem Bogen und einer Sehne liegenden '''Peripheriewinkel''' eines Kreises sind untereinander gleich und halb so groß wie der zugehörige '''Zentriwinkel'''. | ||
Der '''Peripheriewinkel''' der in der Skizze der Winkel Alpha α. Beta β ist der Zentriwinkel. | |||
Demzufolge ist die Aussage: ''α = β/2'' | |||
[[Datei:Peripeherie-Zentri-Winkel.png]] | |||
= Satz des Thales = | = Satz des Thales = | ||
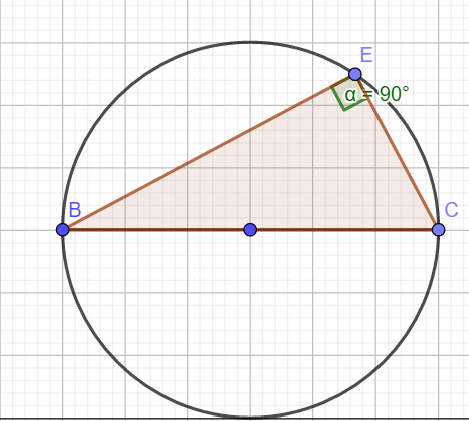
Spezialfall | Ein Spezialfall ist der '''Satz des Thales'''. Ist die Sehne der Durchmesser des Kreises, so ist der Peripheriewinkel 90 Grad. | ||
[[Datei:Satz des Thales.png]] | |||
= Anwendung = | = Anwendung = | ||
Version vom 26. September 2020, 06:48 Uhr
kurze Einleitung
Erkärung
Die über einem Bogen und einer Sehne liegenden Peripheriewinkel eines Kreises sind untereinander gleich und halb so groß wie der zugehörige Zentriwinkel. Der Peripheriewinkel der in der Skizze der Winkel Alpha α. Beta β ist der Zentriwinkel. Demzufolge ist die Aussage: α = β/2
Satz des Thales
Ein Spezialfall ist der Satz des Thales. Ist die Sehne der Durchmesser des Kreises, so ist der Peripheriewinkel 90 Grad.