Würfel: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 2: | Zeile 2: | ||
[[Datei:verschiedene_Spielwürfel.jpg|200px|thumb|right|verschiedene Spielwürfel]] | [[Datei:verschiedene_Spielwürfel.jpg|200px|thumb|right|verschiedene Spielwürfel]] | ||
Würfel gehören zu den [[Quadern]] und sind somit dreidimensionale [[Körper]]. | Würfel gehören zu den [[Quadern]] und sind somit dreidimensionale [[Körper]]. | ||
Ein Würfel ist ein besonderes Quader, weil er von sechs gleichen [[ | Ein Würfel ist ein besonderes Quader, weil er von sechs gleichen [[Vierecke#Quadrate|Quadraten]] begrenzt wird. | ||
Alle Arten von Spielwürfeln mit Zahlen, Buchstaben oder Symbolen werden umgangssprachlich ebenfalls als „Würfel“ bezeichnet. Sie haben verschiedene Formen, wie im zweiten Bild rechts zu sehen ist. | Alle Arten von Spielwürfeln mit Zahlen, Buchstaben oder Symbolen werden umgangssprachlich ebenfalls als „Würfel“ bezeichnet. Sie haben verschiedene Formen, wie im zweiten Bild rechts zu sehen ist. | ||
| Zeile 8: | Zeile 8: | ||
= Lehrplan = | == Lehrplan == | ||
Klasse 1/2, Lernbereich 1: Geometrie | Klasse 1/2, Lernbereich 1: Geometrie | ||
*Kennen von Kugel, Würfel, Quader | *Kennen von Kugel, Würfel, Quader | ||
| Zeile 19: | Zeile 19: | ||
= Beschreibung = | == Beschreibung == | ||
[[Datei:Kantenmodell.jpg|150px|thumb|right|Kantenmodell]] | [[Datei:Kantenmodell.jpg|150px|thumb|right|Kantenmodell]] | ||
Ein Würfel hat sechs Seitenflächen, die alle gleich groß sind und die Form eines [[ | Ein Würfel hat sechs Seitenflächen, die alle gleich groß sind und die Form eines [[Vierecke#Quadrate|Quadrats]] haben. Weil Quadrate die gleiche Seitenlänge haben, sind auch alle Kanten eines Würfels gleich lang. Ein Würfel hat insgesamt 8 Ecken oder Spitzen. An jeder dieser Ecken stoßen drei der quadratischen Seiten aufeinander. | ||
Im Bild rechts ist ein Kantenmodell eines Würfels sehen. | Im Bild rechts ist ein Kantenmodell eines Würfels sehen. | ||
= Würfelnetz = | == Würfelnetz == | ||
[[Datei:Würfelnetz.jpg|200px|thumb|right|Würfelnetz]] | [[Datei:Würfelnetz.jpg|200px|thumb|right|Würfelnetz]] | ||
Ein [[Netz]] ist eine zweidimensionale Darstellung eines geometrischen [[Körper]]s. Wenn man das Netz an den Linien faltet und zusammensetzt, bis die Flächen aneinander liegen, ergibt sich der jeweilige Körper. | Ein [[Netz]] ist eine zweidimensionale Darstellung eines geometrischen [[Körper]]s. Wenn man das Netz an den Linien faltet und zusammensetzt, bis die Flächen aneinander liegen, ergibt sich der jeweilige Körper. | ||
| Zeile 32: | Zeile 32: | ||
Es besteht aus sechs gleichen Quadraten, da diese die Seitenflächen eines Würfels sind. | Es besteht aus sechs gleichen Quadraten, da diese die Seitenflächen eines Würfels sind. | ||
=== Würfelnetze erstellen === | |||
== Würfelnetze erstellen == | |||
Es gibt verschiedene Möglichkeiten, um Würfelnetze selbst herzustellen. | Es gibt verschiedene Möglichkeiten, um Würfelnetze selbst herzustellen. | ||
| Zeile 45: | Zeile 44: | ||
= Übungsaufgabe = | == Übungsaufgabe == | ||
# Erstelle Würfelnetze mithilfe der oben genannten Methoden. Wie viele verschiedene Netze findest du? | # Erstelle Würfelnetze mithilfe der oben genannten Methoden. Wie viele verschiedene Netze findest du? | ||
# Wie viele Kanten hat ein Würfel? Wie viele Kanten zeigen deine erstellen Würfelnetze? Versuche, eine Erklärung zu finden. | # Wie viele Kanten hat ein Würfel? Wie viele Kanten zeigen deine erstellen Würfelnetze? Versuche, eine Erklärung zu finden. | ||
= Quellen = | == Quellen == | ||
Benölken, Ralf / Gorski, Hans-Joachim / Müller-Philipp, Susanne (2018). Leitfaden Geometrie. Für Studierende der Lehrämter. 7., überarbeitete und erweiterte Auflage. Wiesbaden: Springer Spektrum. | Benölken, Ralf / Gorski, Hans-Joachim / Müller-Philipp, Susanne (2018). Leitfaden Geometrie. Für Studierende der Lehrämter. 7., überarbeitete und erweiterte Auflage. Wiesbaden: Springer Spektrum. | ||
Version vom 6. Februar 2021, 16:31 Uhr
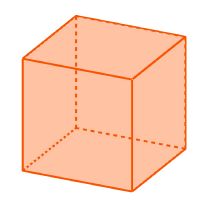

Würfel gehören zu den Quadern und sind somit dreidimensionale Körper. Ein Würfel ist ein besonderes Quader, weil er von sechs gleichen Quadraten begrenzt wird.
Alle Arten von Spielwürfeln mit Zahlen, Buchstaben oder Symbolen werden umgangssprachlich ebenfalls als „Würfel“ bezeichnet. Sie haben verschiedene Formen, wie im zweiten Bild rechts zu sehen ist. Echte Würfel im geometrischen Sinne sind jedoch nur solche Würfel, welche die oben genannte Form haben.
Lehrplan
Klasse 1/2, Lernbereich 1: Geometrie
- Kennen von Kugel, Würfel, Quader
- Würfel als besonderer Quader oder als Körper, der von 6 Quadraten begrenzt wird
Klasse 3, Lernbereich 1: Geometrie
- Übertragen des Wissens über Quader auf das Zeichnen von Würfelnetzen
- Würfel als Sonderfall des Quaders
- handelnd und in der Vorstellung, Falten, Prüfen, Abrollen, Zeichnen
Beschreibung
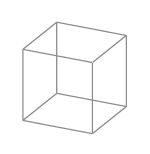
Ein Würfel hat sechs Seitenflächen, die alle gleich groß sind und die Form eines Quadrats haben. Weil Quadrate die gleiche Seitenlänge haben, sind auch alle Kanten eines Würfels gleich lang. Ein Würfel hat insgesamt 8 Ecken oder Spitzen. An jeder dieser Ecken stoßen drei der quadratischen Seiten aufeinander.
Im Bild rechts ist ein Kantenmodell eines Würfels sehen.
Würfelnetz
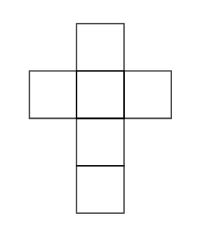
Ein Netz ist eine zweidimensionale Darstellung eines geometrischen Körpers. Wenn man das Netz an den Linien faltet und zusammensetzt, bis die Flächen aneinander liegen, ergibt sich der jeweilige Körper. Das Bild rechts zeigt ein mögliches Würfelnetz. Es besteht aus sechs gleichen Quadraten, da diese die Seitenflächen eines Würfels sind.
Würfelnetze erstellen
Es gibt verschiedene Möglichkeiten, um Würfelnetze selbst herzustellen.
- Lege einen Würfel auf ein Blatt Papier und male den quadratischen Umriss nach. Dann kippe ihn auch eine Seite und male wieder den Umriss nach. Mache dies bei allen Seitenflächen. Am Ende sollten die Umrisse zusammen eine zusammenhängende Fläche aus sechs gleichen Quadraten ergeben.
Tipp: Kennzeichne jede Seite deines Würfels mit einer Farbe, einem Bild oder Aufkleber. Male diesen zum jeweiligen Umriss auf dem Blatt dazu. Auf diese Weise wird erkennbar, welche Seiten schon gemalt sind und wo diese auf dem Blatt zu sehen sind.*
- Anstatt den Umriss zu zeichnen, können die Seiten auch mit Wasserfarbe angemalt werden, sodass beim Kippen ein farbiger Abdruck entsteht. Auf dem Würfel dadurch sichtbar, welche Seiten noch nicht abgebildet wurden. Das Netz zeigt am Ende die zusammenhängenden farbigen Flächen des Würfels.*
Das Ergebnis lässt sich überprüfen, indem man es ausschneidet und zu einem Würfel faltet. Jede Fläche sollte genau einmal vorhanden sein und es dürfen keine Quadrate übereinanderliegen oder Seitenflächen fehlen.
Übungsaufgabe
- Erstelle Würfelnetze mithilfe der oben genannten Methoden. Wie viele verschiedene Netze findest du?
- Wie viele Kanten hat ein Würfel? Wie viele Kanten zeigen deine erstellen Würfelnetze? Versuche, eine Erklärung zu finden.
Quellen
Benölken, Ralf / Gorski, Hans-Joachim / Müller-Philipp, Susanne (2018). Leitfaden Geometrie. Für Studierende der Lehrämter. 7., überarbeitete und erweiterte Auflage. Wiesbaden: Springer Spektrum.
Helmerich, Markus / Lengnink, Katja (2016). Einführung Mathematik Primarstufe – Geometrie. Berlin, Heidelberg: Springer Spektrum.
SMK (2019). Lehrplan Grundschule. Mathematik. Online [02.02.2021].