Multiplikation

Die Multiplikation ist eine der vier Grundrechenarten. Der Begriff stammt aus dem Lateinischen und kann mit dem Wörtern "Vervielfachen" oder "Malnehmen" übersetzt werden.
Das kleine Einmaleins (auch kleines 1x1 genannt) ist besonders wichtig und umfasst alle Multiplikationsaufgaben, die sich aus zwei Zahlen (von 1 bis 10) bilden lassen.

Das kleine Einmaleins

Wichtige Begriffe

Begriffe der Multiplikation

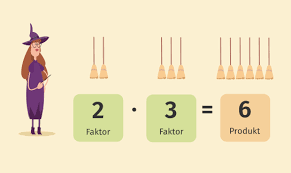
Bei der Multiplikation werden zwei oder mehr Zahlen miteinander multipliziert. Die beiden Zahlen, die miteinander multipliziert werden sollen, nennt man Faktoren.
Wie bei allen anderen Rechenarten (zum Beispiel der Addition oder Subtraktion) gibt es auch für die Multiplikation ein Rechenzeichen. Das Rechenzeichen der Multiplikation ist ein kleiner Punkt ·, den man auch "Malzeichen", "Malpunkt" oder "Multiplikationszeichen" nennt. Der Malpunkt steht immer zwischen den beiden Faktoren.

Das Ergebnis der beiden Faktoren, die miteinander multipliziert wurden, bezeichnet man als Produkt. Zwischen den beiden Faktoren und dem Produkt steht immer das Gleichheitszeichen (=).

Rechenprinzip

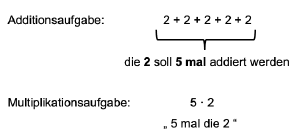
Die Multiplikation benutzt man als Abkürzung für die Addition (+).
Möchte man eine Zahl mehrmals addieren, so lässt sich die Aufgabe durch die Multiplikation verkürzt aufschreiben.
Zu jeder Multiplikationsaufgabe, kann also eine passende Additionsaufgabe gebildet werden.

Die folgenden Links bringen dich zu 2 Videos, in denen dir die Multiplikation nochmal genau erklärt wird:

• https://www.youtube.com/watch?v=giHGDxh82SQ
• https://www.youtube.com/watch?v=wZDgSSBg9Rw

Multiplikation im Alltag

Beispiel: Eis essen

Mama, Papa, Oma, Opa, Tom und Lisa gehen miteinander Eis essen. Heute darf sich jeder 2 Kugeln Eis aussuchen.
Oma lädt die ganze Familie ein. Bevor sie bezahlen kann, muss Oma erst Mal wissen, wie viele Kugeln Eis die Familie insgesamt hat.

Opa erklärt der Oma:

Beispiel: Adventskranz

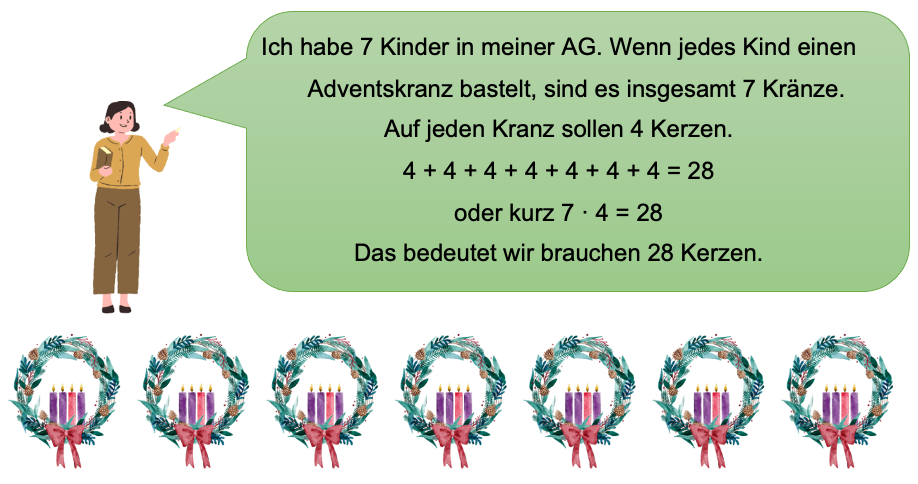
Frau Müller möchte in ihrer AG "Basteln" mit ihren 7 Schülern Adventskränze selber machen. Auf jeden Adventskranz sollen 4 Kerzen.
Frau Müller überlegt, wie viele Kerzen sie braucht, damit jedes Kind einen Adventskranz basteln kann:

Beispiel: Einkaufen

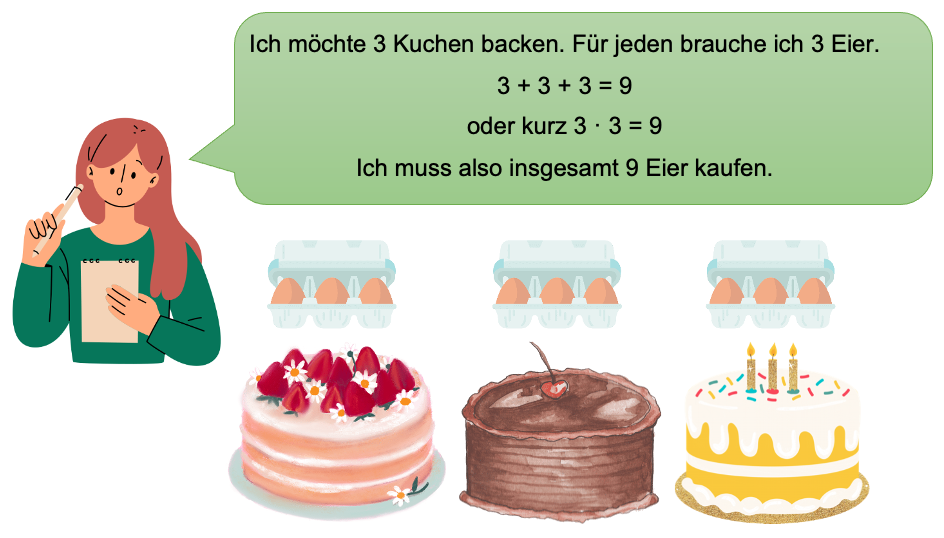
Mama möchte für ihren Geburtstag 3 Kuchen backen. Sie ließt im Rezept, dass sie für jeden Kuchen 3 Eier braucht.
Mama überlegt, wie viele Eier sie insgesamt einkaufen muss:

Besondere Rechenregeln

Vertauschungsgesetz

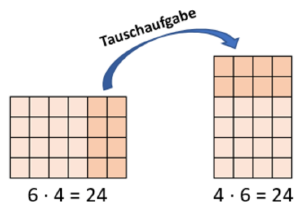
Faktoren dürfen vertauscht werden (Vertauschungsgesetz)

Bei Multiplikationsaufgaben gilt das Vertauschungsgesetz. Das bedeutet:

Bei der Multiplikation können die Faktoren vertauscht werden. Das Ergebnis (Produkt) bleibt gleich.

Zu jeder Multiplikationsaufgabe, lässt sich also immer eine Tauschaufgabe finden.
Der folgende Link bringt dich zu einem Video, in dem dir die Tauschaufgaben nochmal genau erklärt werden:

• https://www.youtube.com/watch?v=NumBAa1XuX0

Multiplikation mit dem Faktor 0

Bei der Multiplikation mit einem Faktor 0 ist zu beachten: Ist ein Faktor 0, so ist das Produkt auch immer 0.

Die Rechenregel lässt sich erkennen, wenn man sich verschiedene Multiplikationsaufgaben mit einem Faktor 0 überlegt und die passenden Additionsaufgaben dazu bildet:

Multiplikationsaufgabe	Additionsaufgabe	Ergebnis
1 · 0	0	0
2 · 0	0 + 0	0
3 · 0	0 + 0 + 0	0
4 · 0	0 + 0 + 0 + 0	0
5 · 0	0 + 0 + 0 + 0 + 0	0
6 · 0	0 + 0 + 0 + 0 + 0 + 0	0
7 · 0	0 + 0 + 0 + 0 + 0 + 0 + 0	0
8 · 0	0 + 0 + 0 + 0 + 0 + 0 + 0 + 0	0
9 · 0	0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0	0
10 · 0	0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0	0

Der folgende Link bringt dich zu einem Video, in dem dir die Multiplikation mit dem Faktor 0 nochmal genau erklärt wird:

• https://www.youtube.com/watch?v=yCeykOxv9dk

Multiplikation mit dem Faktor 1

Multipliziert man eine Zahl mit dem Faktor 1, so ist das Produkt immer die Zahl selbst.

Die Rechenregel lässt sich erkennen, wenn man sich verschiedene Multiplikationsaufgaben mit dem Faktor 1 überlegt und die passenden Additionsaufgaben dazu bildet:

Multiplikationsaufgabe	Additionsaufgabe	Ergebnis
1 · 1	1	1
2 · 1	1 + 1	2
3 · 1	1 + 1 + 1	3
4 · 1	1 + 1 + 1 + 1	4
5 · 1	1 + 1 + 1 + 1 + 1	5
6 · 1	1 + 1 + 1 + 1 + 1 + 1	6
7 · 1	1 + 1 + 1 + 1 + 1 + 1 + 1	7
8 · 1	1 + 1 + 1 + 1 + 1 + 1 + 1 + 1	8
9 · 1	1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1	9
10 · 1	1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1	10

Internetseiten zum Üben des kleinen 1x1

• Malaufgaben im Alltag
• Malaufgaben in der Umwelt
• Aufgabenpaare finden
• Aufgaben ausrechnen und zuordnen
• Tauschaufgaben-Memory
• Tauschaufgaben: Paare finden