Spiegelung: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 6: | Zeile 6: | ||
Der Abstand der Figuren zur [[Spiegelachse]] ist gleich. | Der Abstand der Figuren zur [[Spiegelachse]] ist gleich. | ||
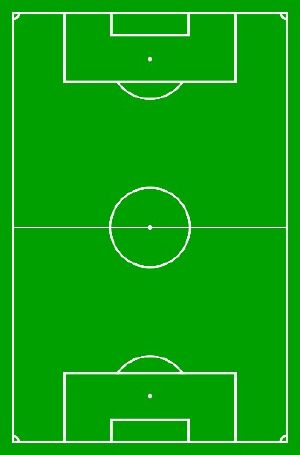
Stellt man sich zum Beispiel vor, das Fußballfeld einmal zu falten, passen beide Seiten genau aufeinander. | Stellt man sich zum Beispiel vor, das Fußballfeld einmal zu falten, passen beide Seiten genau aufeinander. | ||
[[Datei:Feld.jpg|mini|left|Beispiel für Symmetrie in der Umwelt - Fußballfeld]] | |||
==Spiegelachse== | ==Spiegelachse== | ||
[[Datei:Pfeil.jpg| | [[Datei:Pfeil.jpg|mini|right|Pfeil mit horizontaler Spiegelachse]] | ||
Die Spiegelachse einer symmetrischen Figur kann waagrecht oder senkrecht verlaufen. Die Spiegelachse dieses Pfeils verläuft waagerecht. | |||
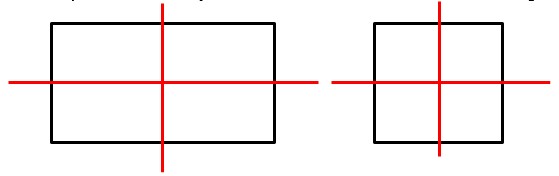
Es gibt auch Figuren, die mehrere Spiegelachsen besitzen. Ein Rechteck hat immer zwei Spiegelachsen und ein Quadrat sogar vier. | Es gibt auch Figuren, die mehrere Spiegelachsen besitzen. Ein Rechteck hat immer zwei Spiegelachsen und ein Quadrat sogar vier. | ||
[[Datei:Vierecke.jpg]] | [[Datei:Vierecke.jpg]] | ||
== | == symmetrische Figuren == | ||
Eine Figur mit einer [[Spiegelachse]] und zwei deckungsgleichen Teilen, ist achsensymmetrisch. | Eine Figur mit einer [[Spiegelachse]] und zwei deckungsgleichen Teilen, ist achsensymmetrisch. | ||
=== Symmetrie in der Umwelt === | === Symmetrie in der Umwelt === | ||
[[Datei:Kleks.jpg|mini|left|Klecksbilder zur Herstellung symmetrischer Figuren]] | |||
[[Datei:Schmetterling.jpg|mini|Beispiel für Symmetrie in der Umwelt - Schmetterling]] | [[Datei:Schmetterling.jpg|mini|Beispiel für Symmetrie in der Umwelt - Schmetterling]] | ||
| Zeile 26: | Zeile 28: | ||
[[Datei:Schild.jpg|mini|Beispiel für Symmetrie in der Umwelt - Verkehrsschilder]] | [[Datei:Schild.jpg|mini|Beispiel für Symmetrie in der Umwelt - Verkehrsschilder]] | ||
Wir können Symmetrie jeden Tag in Unserer Umwelt entdecken. Einige Beispiele sind hier aufgelistet. | Wir können [[Symmetrie]] jeden Tag in Unserer Umwelt entdecken. Einige Beispiele sind hier aufgelistet. | ||
Um [[symmetrische Figuren]] selbst herzustellen kann man zum Beispiel Klecksbilder einmal falten, so entsteht ein deckungsgleiches Bild. Die Faltlinie bildet die [[Spiegelachse]]. | |||
| Zeile 33: | Zeile 38: | ||
[[Datei:lehrplan.jpg]] | [[Datei:lehrplan.jpg]] | ||
Version vom 23. Januar 2020, 19:08 Uhr
Spiegelung
Den Vorgang, der ein Bild mit Hilfe einer Spiegelachse produziert, nennt man Spiegelung . Man kann sich also vorstellen, dass man sich selbst im Spiegel betrachtet. Der Spiegel gibt ein identisches Bild (seitenverkehrt), nämlich das Spiegelbild, wieder. Den eigenen Körper und das Spiegelbild kann man dann deckungsgleich nennen. Ähnlich ist es auch bei Figuren. Diese werden an einer Achse gespiegelt. Dies nennt mann Spiegelachse. Ob eine Figur deckungsgleich ist kann man überprüfen, indem man die Figur faltest. Passen beide Teile genau aufeinander, ist die Figur deckungsgleich. Die entstandene Faltline der Figur ist die Spiegelachse. Der Abstand der Figuren zur Spiegelachse ist gleich. Stellt man sich zum Beispiel vor, das Fußballfeld einmal zu falten, passen beide Seiten genau aufeinander.
Spiegelachse
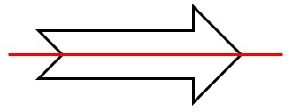
Die Spiegelachse einer symmetrischen Figur kann waagrecht oder senkrecht verlaufen. Die Spiegelachse dieses Pfeils verläuft waagerecht.
Es gibt auch Figuren, die mehrere Spiegelachsen besitzen. Ein Rechteck hat immer zwei Spiegelachsen und ein Quadrat sogar vier.
symmetrische Figuren
Eine Figur mit einer Spiegelachse und zwei deckungsgleichen Teilen, ist achsensymmetrisch.
Symmetrie in der Umwelt

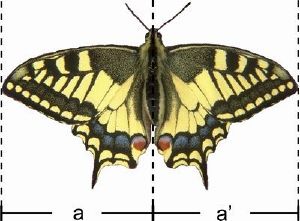


Wir können Symmetrie jeden Tag in Unserer Umwelt entdecken. Einige Beispiele sind hier aufgelistet.
Um symmetrische Figuren selbst herzustellen kann man zum Beispiel Klecksbilder einmal falten, so entsteht ein deckungsgleiches Bild. Die Faltlinie bildet die Spiegelachse.
