Bündelungen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 8: | Zeile 8: | ||
Das Bündeln in der Grundschule dient als Einstieg in das Stellenwertsystem und die damit verbundene Stellenwerttafel. | Das Bündeln in der Grundschule dient als Einstieg in das Stellenwertsystem und die damit verbundene Stellenwerttafel. | ||
Die Einheiten, nach denen gebündelt wird, sind: | Die Einheiten, nach denen gebündelt wird, sind: [[Datei:Bündelungen.png|mini|Einheitenstrukturierung]] | ||
*Einer (E) | *Einer (E) [[Datei:Zehnersystem.png|mini|Zehnersystem]] | ||
*Zehner (Z) | *Zehner (Z) | ||
*Hunderter (H) | *Hunderter (H) | ||
*Tausender (T) | *Tausender (T) | ||
*Zehntausender (ZT) | *Zehntausender (ZT) | ||
Dabei gilt immer: Zehn Einheiten eines Wertes ergeben immer den nächst höheren Wert. | Dabei gilt immer: Zehn Einheiten eines Wertes ergeben immer den nächst höheren Wert. | ||
| Zeile 20: | Zeile 20: | ||
Also: 10 Einer ergeben 1 Zehner, 10 Zehner ergeben 1 Hunderter usw. | Also: 10 Einer ergeben 1 Zehner, 10 Zehner ergeben 1 Hunderter usw. | ||
Das Bündeln wird in der Grundschule meist mit den | Das Bündeln wird in der Grundschule meist unter anderem mit den Teilen des Zehnersystems verdeutlicht. | ||
== Beispiele == | == Beispiele == | ||
(Einzelne Eier werden zu 10er Packungen gebündelt) | |||
[[Datei:Eieraufgabe.png]] | |||
(Einzelne Elemente sollen zu vorgegebenen Päckchen gebündelt werden) | |||
[[Datei:Beispiel.png]] | |||
Natürlich können auch Aufgaben mit den Teilen des Zehnersystem gestellt werden: | |||
*"Lege zwei Zehner und drei Einer!" | |||
*"Lege drei Zehner und neun Einer!" | |||
*Die Lehrkraft legt 15 Einer auf den Tisch und gibt den Auftrag zum Bündeln. | |||
Durch die Bündelungen in größerer Einheiten, lässt sich auch einfacher in größeren Zahlenräumen rechnen. So lässt sich die Additionsaufgabe 36 + 23 zerlegen in: | Durch die Bündelungen in größerer Einheiten, lässt sich auch einfacher in größeren Zahlenräumen rechnen. So lässt sich die Additionsaufgabe 36 + 23 zerlegen in: | ||
Version vom 26. Januar 2020, 12:08 Uhr
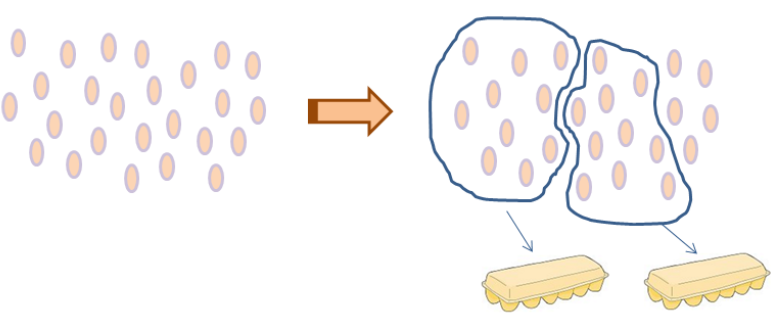
Beim Bündeln wird eine bestimmte Anzahl an Elementen zu einer Teilmenge (einem Bündel) zusammengefasst. Die Elemente, die nach dem Bündeln übrig bleiben, müssen weniger sein, als die Elemente in einem Bündel. Durch dieses Prinzip lassen sich größere ungeordnete Zahlenmengen überschaubar machen. Durch die Bündelungen erhalten die SchülerInnen einen Einblick in die Zahlenwelt.
Das Gegenprinzip zum Bündeln ist das Entbündeln, bei dem die Teilmengen wieder in einzelne Elemente aufgeteilt werden.
Bündelungen in der Grundschule
Das Bündeln in der Grundschule dient als Einstieg in das Stellenwertsystem und die damit verbundene Stellenwerttafel.
Die Einheiten, nach denen gebündelt wird, sind:
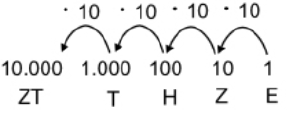
Dabei gilt immer: Zehn Einheiten eines Wertes ergeben immer den nächst höheren Wert.
Also: 10 Einer ergeben 1 Zehner, 10 Zehner ergeben 1 Hunderter usw.
Das Bündeln wird in der Grundschule meist unter anderem mit den Teilen des Zehnersystems verdeutlicht.
Beispiele
(Einzelne Eier werden zu 10er Packungen gebündelt)
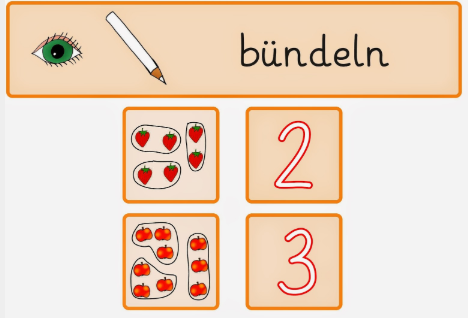
(Einzelne Elemente sollen zu vorgegebenen Päckchen gebündelt werden)
Natürlich können auch Aufgaben mit den Teilen des Zehnersystem gestellt werden:
- "Lege zwei Zehner und drei Einer!"
- "Lege drei Zehner und neun Einer!"
- Die Lehrkraft legt 15 Einer auf den Tisch und gibt den Auftrag zum Bündeln.
Durch die Bündelungen in größerer Einheiten, lässt sich auch einfacher in größeren Zahlenräumen rechnen. So lässt sich die Additionsaufgabe 36 + 23 zerlegen in:
- 3 Zehner + 2 Zehner = 5 Zehner
- 6 Einer + 3 Einer = 9 Einer
Daraus ergibt sich dann das Ergebnis 59.
Einzelnachweise
https://grundschule-kapiert.de/buendeln-und-entbuendeln-klasse-2/