Schriftliche Multiplikation

Die schriftliche Multiplikation ist ein Rechenverfahren und eine besondere Form der Multiplikation. Sie vereinfacht das Multiplizieren großer Zahlen. So ist die schriftliche Multiplikation zum Beispiel sehr nützlich, wenn man eine Mal-Aufgabe mit einer dreistelligen Zahl lösen muss. Auch ein Überschlag kann dabei sinnvoll sein, um das berechnete Ergebnis besser auf seine Richtigkeit einschätzen zu können.

Auf dieser Seite wird die schriftliche Multiplikation einer dreistelligen mit einer einstelligen Zahl im Zahlenraum bis 1000 erläutert. Die schriftliche Multiplikation mit zwei- bis dreistelligem zweiten Faktor lernst du in Klassenstufe 4. Der Überschlag wird ebenfalls in einem anderen Artikel thematisiert.

Voraussetzung

Um die schriftliche Multiplikation richtig anwenden zu können, ist es wichtig, folgende Themenbereiche zu beherrschen:

• kleines Einmaleins
• Addition im Zahlenraum bis 100

Die schriftliche Addition brauchst du erst bei der schriftlichen Multiplikation mit zwei- bis dreistelligem zweiten Faktor.

Rechenanleitung

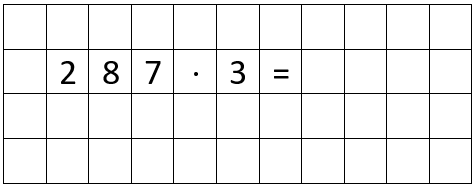
Aufgabe notieren

Bevor du mit dem Rechnen beginnen kannst, musst du dir die Aufgabe in deinen Mathe-Hefter, oder in dein Mathe-Heft notierst. Das Rechnen fällt dir leichter, wenn du für jede Zahl ein eigenes Kästchen benutzt.

Bei der eigentlichen Multiplikation unterscheiden wir in drei Teilrechnungen, die nun Schritt für Schritt erklärt werden.

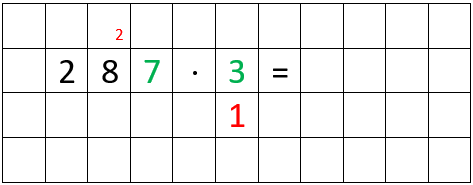
Erste Multiplikation

• Betrachte nur die dritte Ziffer des ersten Faktors, sowie den zweiten Faktor. (GRÜN markiert)
• Diese multiplizierst du miteinander. Du erhältst somit: 7 ⋅ 3 = 21
• Nun notierst du die zweite Ziffer des Ergebnisses, also die 1, unter dem zweiten Faktor, der 3. (ROT markiert)
• Die erste Ziffer des Ergebnisses, also die 2, notierst du über der zweiten Ziffer des ersten Faktors, also über der 8. Das wird Übertrag genannt. (ROT markiert)

Zweite Multiplikation

• Betrachte nur die zweite Ziffer des ersten Faktors, sowie den zweiten Faktor. (GRÜN markiert)
• Diese multiplizierst du miteinander. Du erhältst somit: 8 ⋅ 3 = 24
• Dazu addierst du den Übertrag aus der vorherigen Rechnung. Du rechnest also: 24 + 2 = 26 (GRÜN markiert)
• Nun notierst du die zweite Ziffer des Ergebnisses, also die 6, links neben dem Ergebnis der ersten Multiplikation, also neben der 1. (ROT markiert)
• Die erste Ziffer des Ergebnisses, also die 2, notierst du über der ersten Ziffer des ersten Faktors, also über der 2. Das ist wieder dein Übertrag. (ROT markiert)

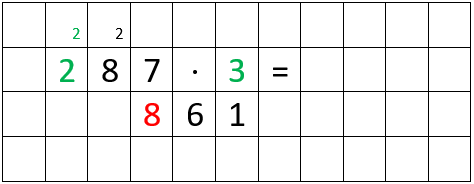
Dritte Multiplikation

• Betrachte nur die erste Ziffer des ersten Faktors, sowie den zweiten Faktor. (GRÜN markiert)
• Diese multiplizierst du miteinander. Du erhältst somit: 2 ⋅ 3 = 6
• Dazu addierst du den Übertrag aus der vorherigen Rechnung. Du rechnest also: 6 + 2 = 8 (GRÜN markiert)
• Nun notierst du das Ergebnis, also die 8, links neben dem bisherigen Ergebnis, also neben der 61. (ROT markiert)

Ergebnis übertragen

Du bist jetzt fertig mit dem Rechnen, allerdings ist die Aufgabe noch nicht komplett fertig. Zum Schluss überträgst du noch dein Ergebnis (GRÜN markiert) in der ersten Zeile neben dem =-Zeichen (ROT markiert).

Besonderheit

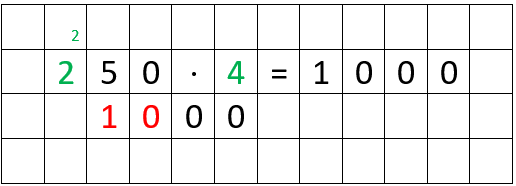
Eine Besonderheit tritt z.B. bei der Aufgabe 250 ⋅ 4 auf. Die ersten beiden Multiplikation werden noch in der Form berechnet, wie es bereits gezeigt wurde. Bei der dritten Multiplikation wird es dann etwas "speziell":

• Betrachte die erste Ziffer des ersten Faktors, sowie den zweiten Faktor. (GRÜN markiert)
• Diese multiplizierst du miteinander. Du erhältst somit: 2 ⋅ 4 = 8
• Dazu addierst du den Übertrag aus der vorherigen Rechnung. Du rechnest also: 8 + 2 = 10 (GRÜN markiert)
• Normalerweise würdest du die erste Ziffer des Ergebnisses, also die 1, als Übertrag notieren. Da du jedoch mit allen drei Multiplikationen fertig bist, kannst du dein Ergebnis, also die 10, direkt links neben den bisherigen Ergebnissen notieren. (ROT markiert)
• Abschließend überträgst du wieder dein Gesamtergebnis.

Übungsaufgaben

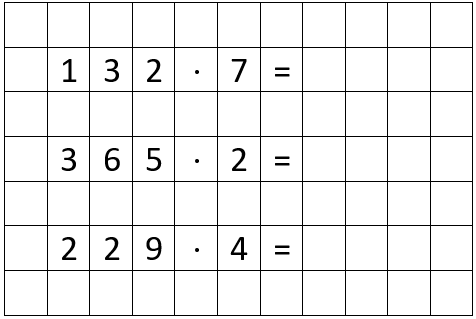
Berechne die folgenden Aufgaben mithilfe der schriftlichen Multiplikation.

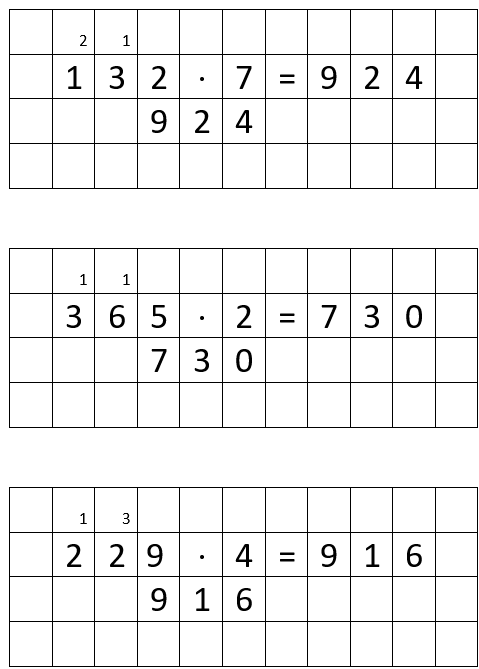
Lösungen

Überprüfe, ob du richtig gerechnet hast. Korrigiere gegebenenfalls deine Berechnungen.