Gleichsinniges und gegenseitiges Verändern (Addition und Subtraktion)

Diese Methode wird in der Addition als auch in der Subtraktion verwendet, um die Rechenoperationen zu vereinfachen. Dabei werden die Zahlen so umgeändert, dass eine einfachere Rechnung entsteht. Sie wird beim halbschriftlichen Rechnen verwendet. Diese Methode funktioniert ähnlich wie beim gleichsinnigen und gegenseitigen Verändern (Multiplikation und Division).

Voraussetzungen

Damit diese Strategie angewendet werden kann, sollten die Grundaufgaben der Addition und Subtraktion im Zahlenraum bis 20 beherrscht werden.

Gegensinniges Verändern bei der Addition

beim 1. Summand wird 7 addiert, beim 2. Summand 7 subtrahiert

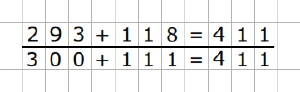
Um die Strategie durchzuführen, muss der ein Summand um eine bestimmte Zahl vergrößert und der andere Summand um diese bestimmte Zahl verkleinert werden. Damit bleibt die Summe erhalten. Ein Summand sollte so verändert werden, dass er ein Vielfaches von 10 wird. Dadurch wird das Rechnen erleichtert.

• So wird bei der Aufgabe 6 + 8 eine Zahl um 2 verkleinert und die andere um 2 vergrößert. Die Aufgabe 4 + 10 entsteht.
• Bei der Aufgabe 33 + 15 gibt es 2 Möglichkeiten für das Verändern.
  • Von der 33 werden 3 abgezogen, wodurch die Zahl 30 entsteht. Zu der 15 werden 3 addiert. Es entsteht die Zahl 18. Die einfache Rechnung 30 + 18 ist entstanden.
  • Von der 15 werden 5 abgezogen und es entsteht die Zahl 10. Zu der 33 werden 5 addiert. Die Rechnung 38 + 10 entsteht.

Bei der Strategie muss auf die Verkleinerung des einen Summanden geachtet werden, da dadurch eine Subtraktionsaufgabe entstehen könnte, die über den Zehner hinausgeht, was die Aufgabe wieder erschweren würde.

• Bei der Aufgabe 33 + 15 könnte man aus der 15 eine 20 machen, die ein Vielfaches von 10 ist. Dadurch müsste man jedoch 5 von 33 subtrahieren, was Schwierigkeiten mit sich bringen kann.

Gleichsinniges Verändern bei der Subtraktion

Gleichsinniges Verändern bei größeren Zahlen: Zu beiden Zahlen wird 5 addiert

Gleichsinniges Verändern bei größeren Zahlen: Von beiden Zahlen wird 7 subtrahiert

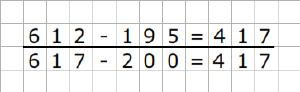
Wie der Name bereits sagt, werden bei dieser Strategie beide Zahlen um die gleiche Zahlen vergrößert oder verkleinert. Die Differenz ändert sich dabei nicht. Dabei sollte die Aufgabe so verändert werden, dass der Subtrahend ein Vielfaches von 10 ist.

• Bei der Aufgabe 15 - 8 wird die Aufgabe so verändert, dass der Subtrahend 10 ergibt. Zu beiden Zahlen wird also 2 addiert. Es entsteht die Aufgabe 17 - 10. Die Differenz von 7 ist somit leichter zu berechnen.

• Bei der Aufgabe 47 - 23 wird die Aufgabe so verändert, dass der Subtrahend 20 ergibt. Von beiden Zahlen wird 3 subtrahiert. Die Aufgabe 44 - 20 entsteht. Das Ergebnis dieser Rechnung ist schnell als 24 erkennbar. Somit ist die Aufgabe 47 - 23 gelöst.

Wie beim gegensinnigen Verändern muss hier darauf geachtet werden, dass die Zwischenrechnungen keinen Zehnerübergang hervorbringen.

• Bei der Aufgabe 47 - 23 wäre es auch möglich, die 23 zu einer 30 zu verändern. Somit würde die Zwischenrechnung 47 + 7 entstehen, die für manche Schülerinnen und Schüler schwieriger sein kann.