Quader

Quader

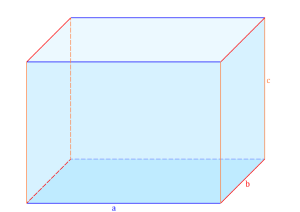
Ein Quader ist ein Körper mit einer rechtwinkligen Grundfläche.Ein besonderer Quader ist der Würfel.

Eigenschaften

Das Quader besitzt folgende Eigenschaften:

• Er besitzt 8 Ecken und 12 Kanten.
• Die vier gegenüberliegenden Kanten sind gleich lang und parallel.
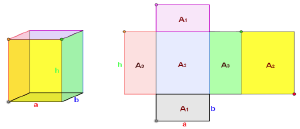
• Ein Quader hat 6 Begrenzungsflächen (Rechtecke), die gegenüberliegenden Seiten sind immer gleich groß und parallel (A1=A1; A2=A2; A3=A3). Man nennt diese Seiten auch kongruent (deckungsgleich).
• Alle Kanten eines Quaders stehen senkrecht im rechten Winkel aufeinander.
• Die Kanten (oder auch Seiten) a, b und c geben die Höhe, Breite und Tiefe des Quaders an.
• Jede Fläche (A1, A2, A3) des Quaders besitzt 2 Flächendiagonalen. Also besitzt der Quader insgesamt 12 Flächendiagonalen, vier gegenüberliegenden sind gleich lang.
• Der Quader besitzt auch einen Mittelpunkt. Er entsteht durch den Schnittpunkt der 4 Raumdiagonalen. Auch diese sind gleich lang.
• Der dreidimensionale Quader lässt sich auch zweidimensional als Quadernetz darstellen.

Quader und Quadernetz

Quader im Alltag

Beispiele im Alltag sind unter anderen:

• Tetrapack
• Schrank
• Brotbüchse
• Legosteine
• Geschirrspültabs
• Spielkartenbox
• Würfel (als eine besondere Form des Quaders)

Berechnungen am Quader

Quader und Quadernetz

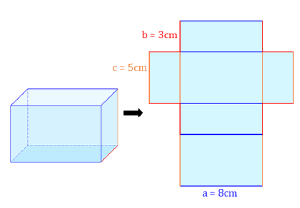
Wie bei jedem dreidimensionalen Objekt kann man auch bei einem Quader die Oberfläche und das Volumen berechnen.

Oberfläche

Da der Quader aus Rechtecken besteht, lässt sich die Oberfläche eines Quaders mit der folgenden Formel berechnen:

• O=2∙(a∙b + a∙c + b∙c)

Volumen

Um das Volumen des Quaders zu berechnen, lässt sich folgende Formel anwenden:

• V=a∙b∙c

Übungsaufgabe

Gegeben ist ein Quader mit den Seitenlängen a=8cm, b=3cm und c=5cm. Berechne das Volumen.

Literatur

mein-lernen.at (2021). Quader Formeln, Eigenschaften und Beispiele. https://www.mein-lernen.at/component/content/article?id=933:quader [10.03.2021]