Satz des Thales
Der Satz des Thales ist ein Satz der Geometrie. Er besagt, dass alle Dreiecke, von denen eine Seite den Durchmesser eines Kreises bildet, rechtwinklig sind. Damit ist er genau genommen ein Spezialfall des Peripherie-Zentriwinkel-Satzes.
Formulierung des Satzes

Sei ∆ABC ein Dreieck. Liegt die C auf dem Kreis mit Durchmesser AB, dann hat das Dreieck bei C einen rechten Winkel. Der Satz lässt sich umkehren und lautet dann: Hat das Dreieck ∆ABC einen rechten Winkel bei C, dann liegt C auf einem Kreis mit Durchmesser AB. [1]
Beweis
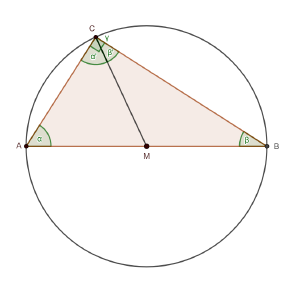
Indem wir vom Mittelpunkt M zu Punkt C den Radius einzeichnen können wir das Dreieck ∆ABC in zwei gleichschenklige Dreiecke ∆AMC und ∆BMC zerlegen, da sowohl die Strecken MA und MC sowie MB und MC den Radius darstellen. Das ursprüngliche Dreieck ∆ABC besitzt wie alle Dreiecke die Innenwinkelsumme 180° Es gilt also: α + β + γ = 180° Da sich der Winkel γ aus α‘ und β‘ ergibt gilt ebenfalls: α + β + (α‘ + β‘) = 180° Die Dreiecke ∆AMC und ∆BMC sind gleichschenklig, woraus folgt, dass α = α‘ und β = β‘ gelten. Wir können also weiter umformen: α + β + (α + β) = 180° Was gleichbedeutend ist mit: 2 ⋅ (α + β) = 180° Teilen wir nun noch durch 2 erhalten wir: α + β = 90°. Da α‘ und β‘ zusammen genauso groß sind wie γ, gilt dies auch für α und β (gleichschenklige Dreiecke). Damit ergibt sich die gesuchte Aussage: γ = 90° [2]
Anwendung
Der Satz des Thales lässt sich unter anderem ausnutzen, um rechtwinklige Dreiecke oder Tangenten an einen Kreis zu konstruieren.
Übung
Bestimme die fehlenden Winkelgrößen.
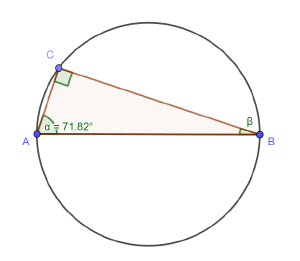
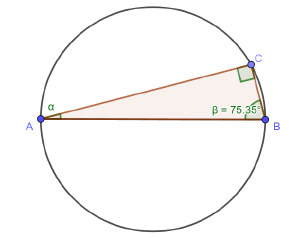
Quellen
- ↑ Scheid H., Schwarz W. Elemente der Geometrie, S. 26 f
- ↑ https://www.studienkreis.de/mathematik/satz-des-thales/#beweis-des-thalessatzes