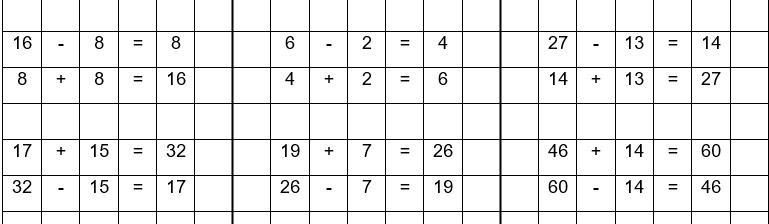Umkehraufgaben
Umkehraufgaben sind entweder Additionsaufgaben (Plusaufgaben), die in Subtraktionsaufgaben (Minusaufgaben) umgewandelt werden, oder Subtraktionsaufgaben, die in Additionsaufgaben umgewandelt werden.
Es gibt auch Umkehraufgaben, bei denen eine Multiplikationsaufgabe (Malaufgabe) in eine Divisionsaufgabe (Geteilt-durch-Aufgabe) oder eine Divisionsaufgabe in eine Multiplikationsaufgabe umgewandelt wird. Darüber kannst etwas du bei Umkehraufgaben mit Multiplikation und Division nachlesen.
Anwendung
Um Umkehraufgaben lösen zu können, muss man die grundlegenden Rechenarten Subtraktion und Addition beherrschen.
Umkehraufgaben werden verwendet, um Lösungen für eine Aufgabe leichter zu finden.
Beispiel:
Aufgabe: 28 - __ = 12
Umkehraufgabe: 12 + __ = 28
Lösung: 12 + 16 = 28, also: 28 - 16 = 12
Sie können aber auch genutzt werden, um eine gefundene Lösung auf Rechenfehler zu überprüfen.
Beispiel:
Aufgabe: 15 + 8 = 23
Umkehraufgabe: 23 - 8 = 15
Also ist die Aufgabe richtig.
Die Zahlen, die dabei verwendet werden, bleiben gleich.
Achtung: Umkehraufgaben sind keine Tauschaufgaben. Da bei Tauschaufgaben die Rechenzeichen gleich bleiben und nur die Zahlen vor dem Ist-gleich-Zeichen ("=") getauscht werden.
Beispielaufgaben
Übungsaufgaben
Versuche nun selbst die Umkehraufgabe zu finden:
Errechne jetzt mit der Umkehraufgabe die Lösung.
Lösungen:
16 - 3 = 13 also: 13 + 3 = 16
32 - 20 = 12 also: 12 + 20 = 32
20 - 5 = 15 also: 15 + 5 = 20
29 + 6 = 35 also: 35 - 6 = 29
18 + 3 = 21 also: 21 - 3 = 18
15 + 19 = 34 also: 34 - 19 = 15
Einzelnachweise
https://www.gut-erklaert.de/mathematik/umkehraufgaben-klasse-1-2.html