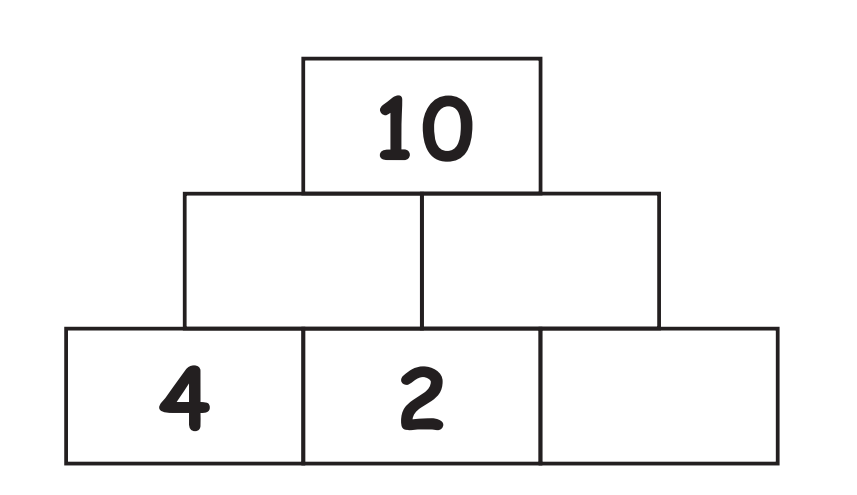
Zahlenmauer
Eine Zahlenmauer - auch Zahlendreieck, Zahlenturm oder Zahlenpyramide genannt - ist ein didaktisches Mittel zum Erlernen der Addition, welches häufig in der Grundschule eingesetzt wird. Der Aufbau einer gewöhnlichen Zahlenmauer ist pyramidenförmig und folgt der Regel: In jedem Feld steht die Summe der beiden darunter stehenden Zahlen. Als häufige Abwandlung gibt es die Subtraktionsmauer und Multiplikationsmauer.
Grundlegendes Prinzip
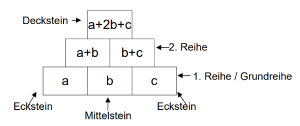
Für Mauern mit drei Reihen gilt:
Der Deckstein ist die Summe der beiden äußeren Grundsteine plus das Doppelte des mittleren Grundsteins.
- Vergrößert man einen der beiden äußeren Grundsteine um 1 (bzw. um 2, 3, 4,...), so wird der Deckstein um 1 (bzw. um 2, 3, 4,...) größer.
- Vergrößert man den mittleren Grundstein um 1 (bzw. um 2, 3, 4,...), so wird der Deckstein um 2 (bzw. um 4, 6, 8,...) größer.
- Sind die äußeren Grundsteine a und c beide gerade Zahlen (oder beide ungerade), dann ist der Deckstein eine gerade Zahl. Ist einer der beiden äußeren Grundsteine gerade und der andere ungerade, dann ist der Deckstein eine ungerade Zahl.
Eine Zahlenmauer kann beliebig groß sein.
Für Mauern mit vier Reihen gilt:
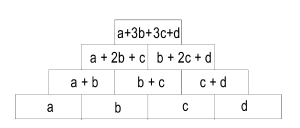
Der Deckstein ist die Summe der beiden äußeren Grundsteine plus die dreifache Summe der beiden inneren Grundsteine.
- Vergrößert man einen der beiden äußeren Grundsteine um 1 (bzw. um 2, 3, 4,...), so wird der Deckstein um 1 (bzw. um 2, 3, 4,...) größer.
- Vergrößert man einen der beiden inneren Grundsteine um 1 (bzw. um 2, 3, 4,...), so wird der Deckstein um 3 (bzw. um 6, 9, 12,...) größer.
Die algebraische Darstellung in den Abbildungen dienen als Hintergrundwissen für die Lehrperson und eignen sich nicht zum Einsatz im Unterricht der Grundschule.
Zahlenmauern in der Mathedidaktik
Mit Zahlenmauern lassen sich sowohl inhaltsbezogene als auch prozessbezogene Kompetenzen fördern:
Inhaltsbezogene Kompetenzen
- Zahlen und Operationen
- Muster und Strukturen
Prozessbezogene Kompetenzen
- Kommunizieren
- Argumentieren
- Darstellen
- Problemlösen
Die genannten Kompetenzen können gefördert werden, indem Schüler und Schülerinnen...
- Beispiele finden und ihre Beobachtungen aufschreiben;
- ihr Vorgehen beschreiben, begründen und Lösungswege mit anderen vergleichen;
- offene Aufgabenstellungen bearbeiten.
Mit Hilfe dieser Fragestellungen können Schüler und Schülerinnen in ihren Kompetenzen gefördert werden:
- Was kannst du beobachten?
- Was bleibt gleich und was verändert sich?
- Welche Unterschiede kannst du erkennen?
- Kannst du deine Entdeckungen begründen?
Zahlenmauern werden hauptsächlich in der Grundschule eingesetzt. Je nach Anordnung der Zahlen müssen entsprechende Rechenoperationen angewandt werden. Ist die Grundreihe vollständig ausgefüllt, wird ausschließlich die Addition verwendet. Sind die Zahlen jedoch verteilt, wird zusätzlich die Subtraktion zur Lösung benötigt. Auf diese Weise können mit diesem didaktischen Mittel vielfältige Fähigkeiten und Kompetenzen geübt werden. Zudem eignen sich Zahlenmauern für die Differenzierung, um der Heterogenität der Schüler und Schülerinnen gerecht zu werden.
Im folgenden Beispiel müssen durch die Anordnung der Zahlen verschiedene Rechenoperationen angewandt werden.
Aufgabenstellungen
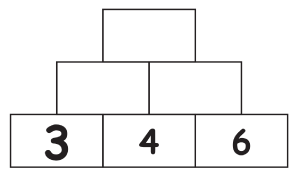
1. Rechne die Zahlenmauer aus.
2. Was passiert mit dem Deckstein, wenn der linke Grundstein um 1 größer wird?
3. Begründe, warum das so ist.
Zahlenmauern in der Unterrichtspraxis
So könnte das kooperative Lernen im Unterricht angeregt werden.
Szene 1: Vier Kinder sitzen an einem Tisch, in der Mitte sind verschiedene Zahlenmauern ausgelegt, welche alle den Deckstein 16 haben. Die Kinder zählen, wie viele verschiedene Zahlenmauern sie finden. Dabei tauschen sie sich darüber aus, wie sie auf ihre Lösungen kommen.
Szene 2: Die Kinder erklären mit einem Partner anhand eines Plakates den Aufbau einer selbst erfundenen Zahlenmauer vor der Klasse.
Literatur
Krauthausen, G.: Zahlenforscher 1: Zahlenmauern. Didaktische Handreichung. Auer, Donauwörth 2006.
TU Dortmund: PIKAS: Zahlenmauern-Übungsheft. In: www.pikas.tu-dortmund.de/upload/Material/Haus_6_Heterogene_Lerngruppen/UM/Zahlenmauern_Uebungsheft/Schueler-Material/Zahlenmauern-Uebungsheft.pdf, Zugriff am 03.02.2021.