Operieren mit Vorstellungsinhalten: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (31 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
Eine Leben ohne die Fähigkeit, sich Dinge vorzustellen, ist nicht möglich. Unsere Vorstellungskraft beginnt bereits, wenn wir uns vorstellen am Strand zu sitzen. Dabei können wir mental die Umgebung um uns erkunden, die Möwen beobachten oder sogar die angenehm warme Wassertemperatur des Meeres auf uns wirken lassen... | Eine Leben ohne die Fähigkeit, sich Dinge vorzustellen, ist nicht möglich. Unsere Vorstellungskraft beginnt bereits, wenn wir uns vorstellen am Strand zu sitzen. Dabei können wir mental die Umgebung um uns erkunden, die Möwen beobachten oder sogar die angenehm warme Wassertemperatur des Meeres auf uns wirken lassen... | ||
Ihr seht, vorstellen können wir uns vieles: Gegenstände und deren Eigenschaften, Beziehungen dieser Gegenstände untereinander und nicht zuletzt Vorgänge und Handlungen. Dabei steht im Fokus nicht das einfache Wiedergeben oder Reproduzieren von Sinneseindrücken, sondern bereits das Wahrnehmen, welches dem Vorstellen vorausgeht. | Ihr seht, vorstellen können wir uns vieles: Gegenstände und deren Eigenschaften, Beziehungen dieser Gegenstände untereinander und nicht zuletzt Vorgänge und Handlungen. Dabei steht im Fokus nicht das einfache Wiedergeben oder Reproduzieren von Sinneseindrücken, sondern bereits das Wahrnehmen, welches dem Vorstellen vorausgeht. | ||
Dieser Artikel beschäftigt sich mit der räumlichen Vorstellungskraft und deren Teilbereiche. | |||
| Zeile 17: | Zeile 19: | ||
== räumliche Beziehungen == | == räumliche Beziehungen == | ||
Die räumliche Beziehunge bezeichnet die Fähigkeit, sich die räumlichen Lagebeziehungen (z. B. dahinter - davor, darüber - darunter, links von - rechts von, zwischen) von unbewegten Objekten vorzustellen. Dabei befindet sich der Standort des Betrachters | Die räumliche Beziehunge bezeichnet die Fähigkeit, sich die räumlichen Lagebeziehungen (z. B. dahinter - davor, darüber - darunter, links von - rechts von, zwischen) von unbewegten Objekten vorzustellen. Dabei befindet sich der Standort des Betrachters außerhalb der räumlichen Situation. Weitere Einzelheiten zu diesem Thema sind in dem Eintrag [[Lagebeziehungsbezeichnungen]] zu finden. | ||
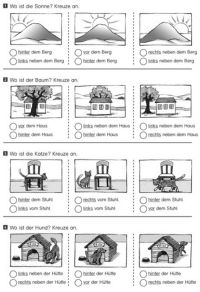
'''Beispiel''' | |||
[[Bild:Lagebeziehungen üben.JPG|200px|Aufgabe zum Üben von Lagebeziehungen]] | |||
== räumliche Orientierung == | == räumliche Orientierung == | ||
Hierbei ist die Fähigkeit gemeint, die eigene Person richtig in eine räumliche Situation einzuordnen, sich real und mental im Raum zurechtzufinden. | Hierbei ist die Fähigkeit gemeint, die eigene Person richtig in eine räumliche Situation einzuordnen, sich real und mental im Raum zurechtzufinden. | ||
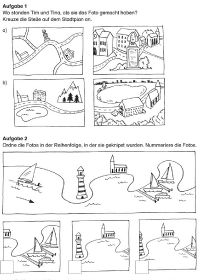
'''Beispiel''' | |||
[[Bild:Lage einer Person.JPG|200px|Aufgaben zum Testen der räumlichen Orientierung]] | |||
== räumliche Visualisierung == | == räumliche Visualisierung == | ||
Unter diesen Begriff versteht man die Fähigkeit, sich Objekte vorzustellen und mit ihnen zu operieren, d. h. sich gedanklich räumliche Bewegungen wie beispielsweise Zerschneiden einer Figur oder räumliche Verschiebungen und Faltungen vorzustellen. | Unter diesen Begriff versteht man die Fähigkeit, sich Objekte vorzustellen und mit ihnen zu operieren, d. h. sich gedanklich räumliche Bewegungen wie beispielsweise Zerschneiden einer [[Figur]] oder räumliche [[Verschiebungen]] und [[Faltungen]] vorzustellen. | ||
'''Beispiele''' | |||
[[Bild:65-figuren-teasing-bild.gif|Aus welchen Teilen setzen sich die Figuren Zusammen (Beispiel für das Zerlegen eines Körpers)]] | |||
Aus welchen Teilen setzen sich die Figuren Zusammen (Beispiel für das Zerlegen eines Körpers) | |||
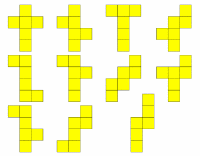
[[Bild:Würfelnetze.gif|200px|Würfelnetze als Beispiel für Faltungen]] | |||
Verschiedene [[Würfel]]netze als Beispiel für Faltungen | |||
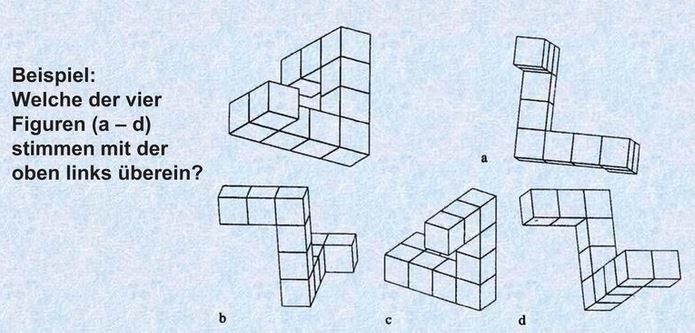
== Vorstellungsfähigkeit von Rotationen == | == Vorstellungsfähigkeit von Rotationen == | ||
Hiermit ist die Fähigkeit | Hiermit ist die Fähigkeit gemeint, sich schnell und präzise [[Rotationen]] (= Drehungen) vorzustellen. | ||
'''Beispiel''' | |||
[[Bild:Mentale Rotation.JPG|Veränderung der Perspektive bei einem Körper durch eine Drehung]] | |||
= Zusammenhang zwischen Vorstellung und Wahrnehmung = | = Zusammenhang zwischen Vorstellung und Wahrnehmung = | ||
Wie sehr unsere Vorstellung durch Wahrnehmungen geprägt ist und wie sehr Vorstellungsleistungen vorangegangene Wahrnehmungen einfordern, verdeutlicht die folgende Abbildung. | Wie sehr unsere Vorstellung durch Wahrnehmungen geprägt ist und wie sehr Vorstellungsleistungen vorangegangene Wahrnehmungen einfordern, verdeutlicht die folgende Abbildung. | ||
[[Bild: Abbildung Würfel.JPG|mini]] | [[Bild: Abbildung Würfel.JPG|mini|Wie nimmst du die Abbildung wahr?]] | ||
* Ein großer Würfel, aus dem ein kleiner Würfel herausgeschnitten wurde? | * Ein großer [[Würfel]], aus dem ein kleiner Würfel herausgeschnitten wurde? | ||
* Der Blick in einen Raum, von dem die hintere und die rechte Wand sowie die Decke zu sehen sind und in dessen hinterer rechter oberer Ecke ein Würfel hängt? | * Der Blick in einen Raum, von dem die hintere und die rechte Wand sowie die Decke zu sehen sind und in dessen hinterer rechter oberer Ecke ein Würfel hängt? | ||
* Ein Würfel, bei dem rechts vorn auf die obere Ecke ein kleiner Würfel aufgesetzt wurde, der jetzt nach vorn zum Betrachter zeigt? | * Ein Würfel, bei dem rechts vorn auf die obere Ecke ein kleiner Würfel aufgesetzt wurde, der jetzt nach vorn zum Betrachter zeigt? | ||
In der Abbildung ist kein Würfel zu sehen. Zu sehen sind nur Flächen und Linien, Sechsecke und Vierecke, darunter sogar ein Quadrat. Die Würfel werden vorgestellt. Wie gut dieses Vorstellen gelingt, hängt wesentlich von den Vorerfahrungen des Betrachters ab. Man entscheidet selbst darüber, welche Vorstellung die einfacherere ist. Jene Vorstellung, die der geläufigeren Wahrnehmung entspricht, setzt sich in der Regel durch. Das erklärt, warum die Vorstellung des Raumes mit dem Würfel in der Ecke vielen von uns schwerer fällt als die Vorstellung des großen Würfels, aus dem ein kleiner Würfel herausgeschnitten wurde. | In der Abbildung ist kein [[Würfel]] zu sehen. Zu sehen sind nur [[Flächen]] und [[Linien]], [[Sechsecke]] und [[Vierecke]], darunter sogar ein [[Quadrat]]. Die Würfel werden vorgestellt. Wie gut dieses Vorstellen gelingt, hängt wesentlich von den Vorerfahrungen des Betrachters ab. Man entscheidet selbst darüber, welche Vorstellung die einfacherere ist. Jene Vorstellung, die der geläufigeren Wahrnehmung entspricht, setzt sich in der Regel durch. Das erklärt, warum die Vorstellung des Raumes mit dem Würfel in der Ecke vielen von uns schwerer fällt als die Vorstellung des großen Würfels, aus dem ein kleiner Würfel herausgeschnitten wurde. | ||
= Anwendungsbereich: Kopfgeometrie = | |||
Bei der [[Kopfgeometrie]] steht nicht das Resultat, sondern der Lösungsprozess im Mittelpunkt. Es soll dabei alle Aufgaben im Kopf gelöst werden. Aus diesem Grund muss man sein räumliches Vorstellungsvermögen einsetzen. | |||
'''Beispiele''' | |||
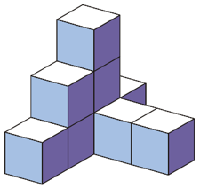
[[Bild:Geometrische figuren.png|200px|Würfelbauwerke]] | |||
"Tom hat mit Würfeln gebaut. Wo hat er mehr Würfel gebraucht? Kreuze an." | |||
Eine genaue Erläuterungen zuspeziell diesem Thema findet man unter dem Eintrag [[Würfelbauwerke]]. | |||
[[Bild:Aufgabe zu Kopfgeometrie.JPG|200px|weitere mögliche Aufgaben zu Würfelbauwerken]] | |||
= Bezug zum sächsischen Lehrplan = | |||
"Operieren mit Vorstellungsinhalten" gehört in den Themenbereich "Kennen von Möglichkeiten zur gedanklichen Orientierung im Raum" des [[sächsischen Lehrplans]] [https://www.schule.sachsen.de/lpdb/web/downloads/10_lp_gs_mathematik_2019.pdf?v2] und wird dem Anfangsunterricht zugeordnet. | |||
Wichtige Aspekte hierbei sind: | |||
* Verändern der Lage und Form, Verschieben, Drehen, Verformen, Zerlegen, Umordnen | |||
* Beschreibung der Veränderungen | |||
= Literatur = | |||
* SÄCHSISCHES STAATSMINISTERIUM FÜR KULTUS (2019). Lehrplan Werken Klasse 1 / 2. https://www.schule.sachsen.de/lpdb/web/downloads/15_lp_gs_mathematik_2019.pdf?v2 | |||
* GRASSMANN, MARIANNE(2014): Mathematikunterricht. 3., korr. u. veränd. Aufl. Baltmannsweiler: Schneider Verl. Hohengehren. | |||
Aktuelle Version vom 6. Februar 2021, 15:55 Uhr
Eine Leben ohne die Fähigkeit, sich Dinge vorzustellen, ist nicht möglich. Unsere Vorstellungskraft beginnt bereits, wenn wir uns vorstellen am Strand zu sitzen. Dabei können wir mental die Umgebung um uns erkunden, die Möwen beobachten oder sogar die angenehm warme Wassertemperatur des Meeres auf uns wirken lassen... Ihr seht, vorstellen können wir uns vieles: Gegenstände und deren Eigenschaften, Beziehungen dieser Gegenstände untereinander und nicht zuletzt Vorgänge und Handlungen. Dabei steht im Fokus nicht das einfache Wiedergeben oder Reproduzieren von Sinneseindrücken, sondern bereits das Wahrnehmen, welches dem Vorstellen vorausgeht.
Dieser Artikel beschäftigt sich mit der räumlichen Vorstellungskraft und deren Teilbereiche.
räumliches Vorstellungsvermögen
Das Wahrnehmen ist ein aktiver Prozess: Was wir wahrnehmen und als was wir etwas wahrnehmen, hängt von unseren Vorerfahrungen und Erwartungen ab. Die Vorstellung kann bereits auf der Grundlage einer verbalen Beschreibung erfolgen. Oft stellen wir uns dreidimensionale Dinge auch auf der Grundlage zweisimensionaler Abbildungen vor: Wir sehen das Urlaubsfoto und erfassen, was dort vor oder hinter dem Strandkorb ist, stellen uns die Sandburg vor, wir sehen eine Bauanleitung und nehmen den Prozess des Bauens in der Vorstellung vorweg. Hier wird die große Bedeutung des räumlichen Vorstellungsvermögens deutlich. Unsere Welt ist dreidimensional, aber alle Möglichkeiten des Aufschreibens, Protokollierens, Fotografierens usw. liefern nur verbale oder zweidimensionale Abbilder. In der Auseinandersetzung mit der Umwelt, bei der Bewältigung von Alltagssituationen ist deshalb immer wieder die Vorstellung räumlicher Objekte, Lagebeziehungen oder Prozesse auf der Grundlage von verbalen Beschreibungen oder zweidimensionaler Abbildungen notwedig:
- beim Überqueren einer Straße und den damit verbundenen Abschätzen von Entfernungen und Geschwindigkeiten herannahender Fahrzeuge
- beim Aufräumen von Dingen in Behälter, Schrankfächer usw.
- beim Bauen mit Bausteinen, Beim Falten nach Faltanleitung
Teilfähigkeiten der räumlichen Vorstellungskraft
räumliche Wahrnehmung
Die räumliche Wahrnehmung bezeichnet die Fähigkeit, Objekte, Lagebeziehungen zwischen Objekten und von Lagebziehungen von Objekten bezüglich des eigenen Körpers wahrzunehmen, zu erfassen. Wir nehmen nicht nur visuell, sondern mit allen Sinnen wahr. Deshalb sind auch Blinde in der Lage, sich Objekte und Prozesse vorzustellen. Sie neigen dazu, sich Längen- oder Lagebeziehungen in Anzahlen von Schritten in einer bestimmte Richtung vorzustellen, während "Sehende" sich eher Bilder und visuelle Merkmale einzelner Objekte vorstellen.
räumliche Beziehungen
Die räumliche Beziehunge bezeichnet die Fähigkeit, sich die räumlichen Lagebeziehungen (z. B. dahinter - davor, darüber - darunter, links von - rechts von, zwischen) von unbewegten Objekten vorzustellen. Dabei befindet sich der Standort des Betrachters außerhalb der räumlichen Situation. Weitere Einzelheiten zu diesem Thema sind in dem Eintrag Lagebeziehungsbezeichnungen zu finden.
Beispiel
räumliche Orientierung
Hierbei ist die Fähigkeit gemeint, die eigene Person richtig in eine räumliche Situation einzuordnen, sich real und mental im Raum zurechtzufinden.
Beispiel
räumliche Visualisierung
Unter diesen Begriff versteht man die Fähigkeit, sich Objekte vorzustellen und mit ihnen zu operieren, d. h. sich gedanklich räumliche Bewegungen wie beispielsweise Zerschneiden einer Figur oder räumliche Verschiebungen und Faltungen vorzustellen.
Beispiele
Aus welchen Teilen setzen sich die Figuren Zusammen (Beispiel für das Zerlegen eines Körpers)
Verschiedene Würfelnetze als Beispiel für Faltungen
Vorstellungsfähigkeit von Rotationen
Hiermit ist die Fähigkeit gemeint, sich schnell und präzise Rotationen (= Drehungen) vorzustellen.
Beispiel
Zusammenhang zwischen Vorstellung und Wahrnehmung
Wie sehr unsere Vorstellung durch Wahrnehmungen geprägt ist und wie sehr Vorstellungsleistungen vorangegangene Wahrnehmungen einfordern, verdeutlicht die folgende Abbildung.
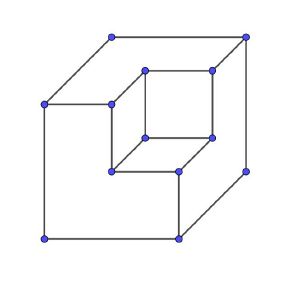
- Ein großer Würfel, aus dem ein kleiner Würfel herausgeschnitten wurde?
- Der Blick in einen Raum, von dem die hintere und die rechte Wand sowie die Decke zu sehen sind und in dessen hinterer rechter oberer Ecke ein Würfel hängt?
- Ein Würfel, bei dem rechts vorn auf die obere Ecke ein kleiner Würfel aufgesetzt wurde, der jetzt nach vorn zum Betrachter zeigt?
In der Abbildung ist kein Würfel zu sehen. Zu sehen sind nur Flächen und Linien, Sechsecke und Vierecke, darunter sogar ein Quadrat. Die Würfel werden vorgestellt. Wie gut dieses Vorstellen gelingt, hängt wesentlich von den Vorerfahrungen des Betrachters ab. Man entscheidet selbst darüber, welche Vorstellung die einfacherere ist. Jene Vorstellung, die der geläufigeren Wahrnehmung entspricht, setzt sich in der Regel durch. Das erklärt, warum die Vorstellung des Raumes mit dem Würfel in der Ecke vielen von uns schwerer fällt als die Vorstellung des großen Würfels, aus dem ein kleiner Würfel herausgeschnitten wurde.
Anwendungsbereich: Kopfgeometrie
Bei der Kopfgeometrie steht nicht das Resultat, sondern der Lösungsprozess im Mittelpunkt. Es soll dabei alle Aufgaben im Kopf gelöst werden. Aus diesem Grund muss man sein räumliches Vorstellungsvermögen einsetzen.
Beispiele
"Tom hat mit Würfeln gebaut. Wo hat er mehr Würfel gebraucht? Kreuze an." Eine genaue Erläuterungen zuspeziell diesem Thema findet man unter dem Eintrag Würfelbauwerke.
Bezug zum sächsischen Lehrplan
"Operieren mit Vorstellungsinhalten" gehört in den Themenbereich "Kennen von Möglichkeiten zur gedanklichen Orientierung im Raum" des sächsischen Lehrplans [1] und wird dem Anfangsunterricht zugeordnet. Wichtige Aspekte hierbei sind:
- Verändern der Lage und Form, Verschieben, Drehen, Verformen, Zerlegen, Umordnen
- Beschreibung der Veränderungen
Literatur
- SÄCHSISCHES STAATSMINISTERIUM FÜR KULTUS (2019). Lehrplan Werken Klasse 1 / 2. https://www.schule.sachsen.de/lpdb/web/downloads/15_lp_gs_mathematik_2019.pdf?v2
- GRASSMANN, MARIANNE(2014): Mathematikunterricht. 3., korr. u. veränd. Aufl. Baltmannsweiler: Schneider Verl. Hohengehren.