Benutzer:Division mit Rest: Unterschied zwischen den Versionen
K GI-WS2021 verschob die Seite Kategorie:Division mit Rest nach Benutzer:Division mit Rest |
|||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Kategorie: Arithmetik]] | |||
== Division mit Rest == | == Division mit Rest == | ||
<br> | <br> | ||
Aktuelle Version vom 19. September 2021, 17:46 Uhr
Division mit Rest
1 Was ist Division mit Rest?
Division mit Rest ist das ziffernweise Zerlegen und Dividieren von Zahlen. Dabeigeht die Divion nicht auf und es entsteht ein Rest.
Dieses Verfahren ist die Vorstufe der schriftlichen Division, siehe Schriftliche Division.
Die Umkehroperation ist die Multiplikation.
2 Warum muss man mit Rest dividieren können?
Division mit Rest braucht man bei Mengen mit nicht teilbaren Objekten, wie z.B. eine Klasse in Gruppen aufteilen.
Besonders in der Grundschule ist diese Methode anzuwenden, da die Schüler und Schülerinnen mit ganzen Zahlen rechnen, nicht mit Kommazahlen/Dezimalzahlen. Nur in den wenigsten Fällen wird schon mit gebrochenen Zahlen gerechnet (wie z.B. 1/2, 1/4, 3/4, ...).
3 Wie Dividiere ich mit Rest?
Beispielaufgabe 96:9=
1) Wie oft passt die 9 (Divisor) in die 9 (Zehner des Dividenten)?
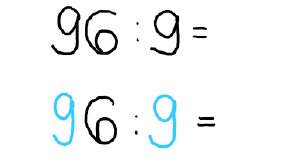
Die 9 passt 1 mal in die 9. -> Schreibe 1.
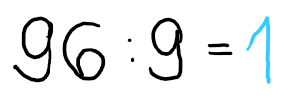
2) Rechne nun 1*9, das ist 9. Schreibe die 9 unter die 9 und subtrahiere.
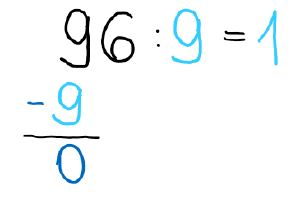
3) Wie oft passt die 9 in die 0?
Die 9 passt nicht in die 0. -> Ziehe die 6 runter.
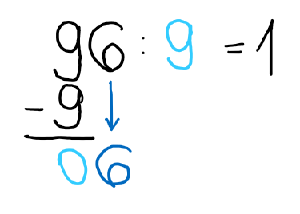
4) Wie oft passt die 9 in die 6?
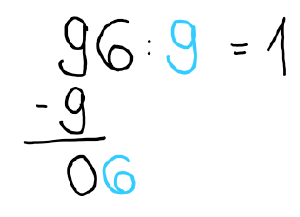
Die 9 passt nicht in die 6. -> Schribe 0.
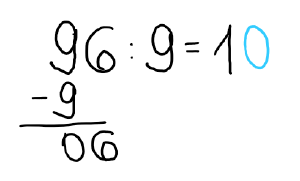
5) Rechne 0*9, das ist 0.
Schreibe die 0 unter die 6 und subtrahiere. -> Es bleiben 6 übrig. Schreibe R6.
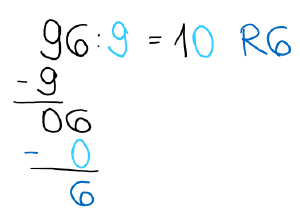
4 Lernvideo
Wiederholung
In diesem Video bekommst du noch einmal die Division mit Rest erklärt. Es sind einfache Aufgaben aus dem Bereich des kleinen 1x1.
Wenn du noch weißt wie das ging, dann musst du dir dieses Vide nicht anschauen.
Schriftliche Division mit Rest
Hier werden mit dir schweirigere Aufgaben gerechnet. Bitte schaue dir wenigstens die ersten Rechenbeispiele an.
5 Übungsaufgaben
Aufgaben im 1x1 Bereich
1. a)
45:6=
67:7=
23:3=
89:9=
17:6=
b)
28:8=
15:5=
37:4=
55:2=
73:10=
Aufgaben im Hunderterbereich
2. a)
187:10=
743:9=
270:8=
729:7=
239:6=
209:5=
130:4=
318:3=
237:2=
278:1=
b)
348:3=
248:6=
103:9=
578:10=
249:8=
137:6=
279:4=
938:2=
827:5=
164:1=
Aufgaben mit Zehner-Divisor im Tausenderbereich
3. a)
2787:36=
2987:23=
1409:89=
1378:36=
1677:37=
b)
95784:26=
49788:29=
40997:92=
40747:29=
52987:23=
6 Lösungen
1. a)
45:6=7 R3
67:7=9 R4
23:3=7 R2
89:9=9 R8
17:6=2 R5
b)
28:8=3 R4
15:5=3 (R0)
37:4=9 R1
55:2=27 R1
73:10=7 R3
2. a)
187:10=18 R7
743:9=82 R5
270:8=44 R6
729:7=104 R1
239:6=39 R5
209:5=41 R4
130:4=32 R2
318:3=106 (R0)
237:2=118 R1
278:1=278 (R0)
b)
348:3=116 (R0)
248:6=41 R2
103:9=11 R4
578:10=57 R8
249:8=31 R1
137:6=22 R5
279:4=69 R3
938:2=469 (R0)
827:5=165 R2
164:1=164 (R0)
3. a)
2787:36=77 R15
2987:23=129 R6
1409:89=15 R74
1378:36=38 R10
1677:37=45 R12
b)
95784:26=3684 (R0)
49788:29=1716 R24
40997:92=445 R57
40747:29=1405 R2
52987:23=2303 R18
7 Zusammenfassung
Wenn wir unsere Klasse in Gruppen, ganze Äpfel und Birnen verteilen oder Blätter austeilen wollen und es nicht im Kopf rechnen können, dann brauchen wir die Methode der schriftlichen Division mit Rest. Für die schriftliche Division mit Kommazahlen (Dezimalzahlen) ist diese Methode eine wichtige Vorstufe. Division mit Rest gibt es in unterschiedlichen Metoden, wie wir vielleicht nebenbei mitbekommen haben. In Klasse 2 und 3 rechneten wir mehr im Kopf, jetzt in einer Form des Schriftlichen. Doch man muss auch die mathematischen Grenzen der Division mit Rest benennen. Wwir betrachten die Aufgaben 17:5=3 R2 und 29:9=3R2. Wir sehen, dass die Ergebnisse scheinbar gleich sind, aber das sind diese nicht. Spätestens bei der schriftlichen Divission sehen wir den Unterschied. Zurück zu den beiden Aufgaben: 3 R2 von 17:5 kann man auch wie folgt schreiben: 3 2/5 und das Ergebnis von 29:9 = 3 2/9. 2/5 und 2/9 ist sichtbar nicht das Gleiche. Schreibt man 3 R2 sieht man den Unterschied nicht. Das müssen wir bei dem Vergleichen von Ergebnissen, z.B. in Sachaufgaben beachten.