Spiegeln: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (18 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
Das Spiegeln kann im Mathematikunterricht nicht bloß hinsichtlich geometrischer Inhalte genutzt werden. Es bietet sich an dies auch unter arithmetischen Gesichtspunkten zu betrachten. | Das '''Spiegeln''' kann im Mathematikunterricht nicht bloß hinsichtlich geometrischer Inhalte genutzt werden. | ||
Es bietet sich an dies auch unter arithmetischen Gesichtspunkten zu betrachten. | |||
Insbesondere schließt sich das Verdoppeln von Zahlenmengen sowie das Untersuchen von Symmetrien in arithmetischen Kontexten an. | Insbesondere schließt sich das Verdoppeln von Zahlenmengen sowie das Untersuchen von Symmetrien in arithmetischen Kontexten an. | ||
= Was bedeutet Spiegeln? = | == Was bedeutet Spiegeln? == | ||
Beim Spiegeln von bestimmten Sachen entsteht stehts ein Spiegelbild dieser Sachen. Steht man zum Beispiel vor einem Spiegel sieht man sich selbst in diesem. [[Datei: Bild spiegel.PNG|mini]] | Beim Spiegeln von bestimmten Sachen entsteht stehts ein Spiegelbild dieser Sachen. | ||
Steht man zum Beispiel vor einem Spiegel sieht man sich selbst in diesem. [[Datei: Bild spiegel.PNG|mini]] | |||
Kommt jedoch nun eine andere Person in den Raum, kann diese einen jedoch zweimal (verdoppelt) sehen, einmal in echt und einmal im Spiegelbild. | Kommt jedoch nun eine andere Person in den Raum, kann diese einen jedoch zweimal (verdoppelt) sehen, einmal in echt und einmal im Spiegelbild. | ||
Dieses Prinzip kann auch auf das Verdoppeln von Objekten angewendet werden. | Dieses Prinzip kann auch auf das Verdoppeln ([[Verdopplung/ Halbierung]]) von Objekten angewendet werden. | ||
== Einsatz von Spiegeln in der Arithmetik== | |||
Wird ein Bild gespiegelt, so wird dieses Bild im Spiegel exakt so abgebildet. | |||
Sind in diesem Bild Mengen zu erkennen oder wird statt dem Bild direkt eine Menge von Objekten (z.B. Legeplättchen) gespiegelt, so bildet sich die Menge genauso wieder ab. | |||
Wenn man das mit dem Spiegeln verbundene Prinzip des Verdoppelns nimmt, so verdoppelt sich also diese Menge. | |||
[[Datei: Zahlendoppel.PNG|mini|left]] | |||
| Zeile 17: | Zeile 37: | ||
Im Unterricht können diese Spiegelmengen in Rechnungen umgewandelt werden. | Im Unterricht können diese Spiegelmengen in Rechnungen umgewandelt werden. | ||
| Zeile 29: | Zeile 46: | ||
Doch nicht bloß in Verbindung mit Mengen können Spiegelungen Zahlen neu darstellen. Auch auf dem Zahlenstrahl kann eine [[Spiegelung]] Zusammenhänge aufzeigen. | |||
Doch nicht bloß in Verbindung mit Mengen können Spiegelungen Zahlen neu darstellen. Auch auf dem Zahlenstrahl | |||
Zum Beispiel können auf diesem Striche als Spiegelachsen eingezeichent werden damit kann erkannt werden, welche beiden Zahlen genau gleichweit von der gespiegelten Zahlen entfernt liegen. | Zum Beispiel können auf diesem Striche als Spiegelachsen eingezeichent werden damit kann erkannt werden, welche beiden Zahlen genau gleichweit von der gespiegelten Zahlen entfernt liegen. | ||
So kann erkannt werden, dass wenn auf dem Zahlenstrahl zwei Zahlen liegen, die sich zu 10 ergänzen, diese symmetrisch zur 5 leigen. Zum Beispiel sind 3 und 7 gleichweit von der 5 entfernt. | So kann erkannt werden, dass wenn auf dem Zahlenstrahl zwei Zahlen liegen, die sich zu 10 ergänzen, diese symmetrisch ([[Symmetrie]])zur 5 leigen. Zum Beispiel sind 3 und 7 gleichweit von der 5 entfernt. | ||
Diese Erkenntnis kann als Hilfsrechnung genutzt werden. | Diese Erkenntnis kann als Hilfsrechnung genutzt werden. | ||
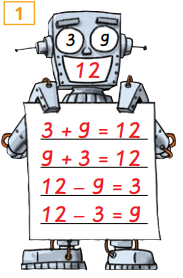
Weiterhin können damit Umkehraufgaben eingeführt werden, sodass beispielsweise mit Hilfe einer Spiegelung aus 9+3 = 12 --> 12= 3+9 wird. [[Datei: Roboter.PNG|mini]] | Weiterhin können damit Umkehraufgaben eingeführt werden, sodass beispielsweise mit Hilfe einer [[Spiegelung]] aus 9+3 = 12 --> 12= 3+9 wird. [[Datei: Roboter.PNG|mini|Umkehraufgaben]] | ||
Aktuelle Version vom 26. Januar 2020, 14:12 Uhr
Das Spiegeln kann im Mathematikunterricht nicht bloß hinsichtlich geometrischer Inhalte genutzt werden. Es bietet sich an dies auch unter arithmetischen Gesichtspunkten zu betrachten. Insbesondere schließt sich das Verdoppeln von Zahlenmengen sowie das Untersuchen von Symmetrien in arithmetischen Kontexten an.
Was bedeutet Spiegeln?
Beim Spiegeln von bestimmten Sachen entsteht stehts ein Spiegelbild dieser Sachen.
Steht man zum Beispiel vor einem Spiegel sieht man sich selbst in diesem.

Kommt jedoch nun eine andere Person in den Raum, kann diese einen jedoch zweimal (verdoppelt) sehen, einmal in echt und einmal im Spiegelbild.
Dieses Prinzip kann auch auf das Verdoppeln (Verdopplung/ Halbierung) von Objekten angewendet werden.
Einsatz von Spiegeln in der Arithmetik
Wird ein Bild gespiegelt, so wird dieses Bild im Spiegel exakt so abgebildet. Sind in diesem Bild Mengen zu erkennen oder wird statt dem Bild direkt eine Menge von Objekten (z.B. Legeplättchen) gespiegelt, so bildet sich die Menge genauso wieder ab. Wenn man das mit dem Spiegeln verbundene Prinzip des Verdoppelns nimmt, so verdoppelt sich also diese Menge.
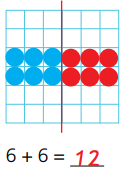
Im Unterricht können diese Spiegelmengen in Rechnungen umgewandelt werden.
Doch nicht bloß in Verbindung mit Mengen können Spiegelungen Zahlen neu darstellen. Auch auf dem Zahlenstrahl kann eine Spiegelung Zusammenhänge aufzeigen. Zum Beispiel können auf diesem Striche als Spiegelachsen eingezeichent werden damit kann erkannt werden, welche beiden Zahlen genau gleichweit von der gespiegelten Zahlen entfernt liegen. So kann erkannt werden, dass wenn auf dem Zahlenstrahl zwei Zahlen liegen, die sich zu 10 ergänzen, diese symmetrisch (Symmetrie)zur 5 leigen. Zum Beispiel sind 3 und 7 gleichweit von der 5 entfernt. Diese Erkenntnis kann als Hilfsrechnung genutzt werden.
Weiterhin können damit Umkehraufgaben eingeführt werden, sodass beispielsweise mit Hilfe einer Spiegelung aus 9+3 = 12 --> 12= 3+9 wird.