Flächeninhalt: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| (7 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
== Flächeneinheiten == | == Flächeneinheiten == | ||
Der Flächeninhalt wird immer in einer bestimmten Flächeneinheit angegeben. In den meisten Ländern nutzt man dafür das [[metrische System]]. Der Flächeninhalt wird dann zum Beispiel in [[Quadratmetern]] angegeben. Ein Quadratmeter entspricht einer Fläche, die einen [[Meter]] lang und einen Meter breit ist. "Ein Quadratmeter" wird so geschrieben: 1[[m²]]. Der Flächeninhalt kann genauso in Quadratzentimetern ([[cm²]]), Quadratmillimetern ([[mm²]]) usw. angegeben werden. | Der Flächeninhalt wird immer in einer bestimmten Flächeneinheit angegeben. | ||
In den meisten Ländern nutzt man dafür das [[metrische System]]. Der Flächeninhalt wird dann zum Beispiel in [[Quadratmetern]] angegeben. Ein Quadratmeter entspricht einer Fläche, die einen [[Meter]] lang und einen Meter breit ist. "Ein Quadratmeter" wird so geschrieben: 1[[m²]]. Der Flächeninhalt kann genauso in Quadratzentimetern ([[cm²]]), Quadratmillimetern ([[mm²]]) usw. angegeben werden. | |||
== Flächeninhalt von Rechtecken== | == Flächeninhalt von Rechtecken== | ||
Am einfachsten kann man einen Flächeninhalt ausrechnen, wenn man es mit einem [[Rechteck]] zu tun hat. Ein Rechteck besitzt vier rechte Winkel und die gegenüberliegenden Seiten sind gleich lang. Jedes Rechteck hat eine [[Länge]] und eine [[Breite]]. In der [[Geometrie]] bezeichnet man sie meistens mit den Kleinbuchstaben a und b. Man erhält den Flächeninhalt A, wenn man die [[Seite]] a mit der Seite b multipliziert. | [[Datei:Rechteck.jpg|mini|Flächeninhalt eines Rechtecks]] | ||
Am einfachsten kann man einen Flächeninhalt ausrechnen, wenn man es mit einem [[Rechteck]] zu tun hat. Ein Rechteck besitzt vier rechte Winkel und die gegenüberliegenden Seiten sind gleich lang. Jedes Rechteck hat eine [[Länge]] und eine [[Breite]]. In der [[Geometrie]] bezeichnet man sie meistens mit den Kleinbuchstaben a und b. | |||
Man erhält den Flächeninhalt A, wenn man die [[Seite]] a mit der Seite b multipliziert. | |||
Man rechnet also: '''A = a ⋅ b''' | Man rechnet also: '''A = a ⋅ b''' | ||
== Flächeninhalt von Quadraten == | == Flächeninhalt von Quadraten == | ||
[[Datei:Quadrat.jpg|mini|Flächeninhalt eines Quadrates]] | |||
[[Quadrate]] sind besondere Rechtecke. Sie besitzen vier rechte Winkel und vier gleich lange Seiten. Die Länge und Breite des Quadrates können deshalb mit demselben Buchstaben bezeichnet werden, zum Beispiel mit dem Kleinbuchstaben a. | |||
Der Flächeninhalt von Quadraten wird genauso berechnet wie der von Rechtecken. | |||
Man rechnet also: '''A = a ⋅ a''' | Man rechnet also: '''A = a ⋅ a''' | ||
| Zeile 28: | Zeile 50: | ||
=== Flächeninhalt eines Rechtecks === | === Flächeninhalt eines Rechtecks === | ||
Angenommen, wir haben ein Rechteck mit der Länge a = 3m und der Breite b = 4m. Dann berechnen wir den Flächeninhalt folgendermaßen: A = a ⋅ b = 3m ⋅ 4m = 12m². Somit beträgt der Flächeninhalt des Rechtecks 12 Quadratmeter, also 12m². | Angenommen, wir haben ein Rechteck mit der Länge a = 3m und der Breite b = 4m. | ||
Dann berechnen wir den Flächeninhalt folgendermaßen: A = a ⋅ b = 3m ⋅ 4m = 12m². | |||
Somit beträgt der Flächeninhalt des Rechtecks 12 Quadratmeter, also 12m². | |||
=== Flächeninhalt eines Quadrates === | === Flächeninhalt eines Quadrates === | ||
Angenommen, wir haben ein Quadrat mit der Seitenlänge a = 5cm. Dann rechnen wir: A = a ⋅ a = 5cm ⋅ 5cm = 25cm². Somit beträgt der Flächeninhalt des Quadrates 25 Quadratzentimeter, also 25cm². | Angenommen, wir haben ein Quadrat mit der Seitenlänge a = 5cm. | ||
Dann rechnen wir: A = a ⋅ a = 5cm ⋅ 5cm = 25cm². | |||
Somit beträgt der Flächeninhalt des Quadrates 25 Quadratzentimeter, also 25cm². | |||
== Übungsaufgabe == | |||
1. Berechne den Flächeninhalt eines Rechtecks mit den Seitenlängen a = 5m und b = 6m. | |||
2. Berechne den Flächeninhalt eines Quadrates mit der Seitenlänge a = 7mm. | |||
Beachte die Einheiten! | |||
[[Kategorie:Geometrie]] | [[Kategorie:Geometrie]] | ||
Aktuelle Version vom 15. März 2021, 16:24 Uhr
Der Flächeninhalt gibt an, wie groß die Fläche von Figuren oder Gebieten in der Ebene ist. Wenn man den Flächeninhalt berechnet, wird das Ergebnis mit dem Großbuchstaben A bezeichnet.
Flächeneinheiten
Der Flächeninhalt wird immer in einer bestimmten Flächeneinheit angegeben.
In den meisten Ländern nutzt man dafür das metrische System. Der Flächeninhalt wird dann zum Beispiel in Quadratmetern angegeben. Ein Quadratmeter entspricht einer Fläche, die einen Meter lang und einen Meter breit ist. "Ein Quadratmeter" wird so geschrieben: 1m². Der Flächeninhalt kann genauso in Quadratzentimetern (cm²), Quadratmillimetern (mm²) usw. angegeben werden.
Flächeninhalt von Rechtecken
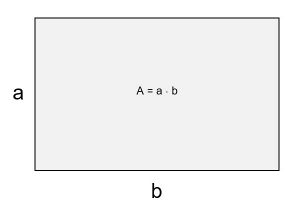
Am einfachsten kann man einen Flächeninhalt ausrechnen, wenn man es mit einem Rechteck zu tun hat. Ein Rechteck besitzt vier rechte Winkel und die gegenüberliegenden Seiten sind gleich lang. Jedes Rechteck hat eine Länge und eine Breite. In der Geometrie bezeichnet man sie meistens mit den Kleinbuchstaben a und b.
Man erhält den Flächeninhalt A, wenn man die Seite a mit der Seite b multipliziert.
Man rechnet also: A = a ⋅ b
Flächeninhalt von Quadraten
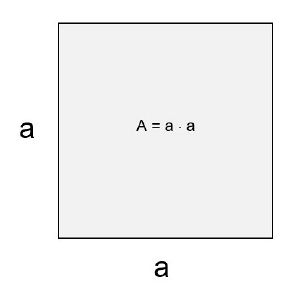
Quadrate sind besondere Rechtecke. Sie besitzen vier rechte Winkel und vier gleich lange Seiten. Die Länge und Breite des Quadrates können deshalb mit demselben Buchstaben bezeichnet werden, zum Beispiel mit dem Kleinbuchstaben a.
Der Flächeninhalt von Quadraten wird genauso berechnet wie der von Rechtecken.
Man rechnet also: A = a ⋅ a
Beispiele für die Berechnung des Flächeninhalts
Flächeninhalt eines Rechtecks
Angenommen, wir haben ein Rechteck mit der Länge a = 3m und der Breite b = 4m.
Dann berechnen wir den Flächeninhalt folgendermaßen: A = a ⋅ b = 3m ⋅ 4m = 12m².
Somit beträgt der Flächeninhalt des Rechtecks 12 Quadratmeter, also 12m².
Flächeninhalt eines Quadrates
Angenommen, wir haben ein Quadrat mit der Seitenlänge a = 5cm.
Dann rechnen wir: A = a ⋅ a = 5cm ⋅ 5cm = 25cm².
Somit beträgt der Flächeninhalt des Quadrates 25 Quadratzentimeter, also 25cm².
Übungsaufgabe
1. Berechne den Flächeninhalt eines Rechtecks mit den Seitenlängen a = 5m und b = 6m.
2. Berechne den Flächeninhalt eines Quadrates mit der Seitenlänge a = 7mm.
Beachte die Einheiten!