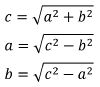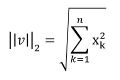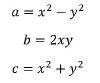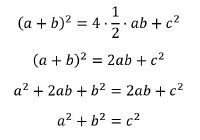Satz des Pythagoras: Unterschied zwischen den Versionen
DiMedS (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
DiMedS (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (30 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
== Geschichte == | == Geschichte == | ||
Der Satz des Pythagoras geht auf den griechischen Philosophen Pythagoras von Samos zurück, der von ca. 50 v. Chr. bis ca. 500 n. Chr. gelebt hat.<ref>https://de.bettermarks.com/mathe/pythagoras-von-samos/</ref> Pythagoras von Samos war ein griechischer Gelehrter und Philsoph und ist unter anderem noch für die nach ihm benannte Strömung der Pythagoreer bekannt. Der Satz des Pythagoras gilt dennoch als sein wichtigstes Erbe, welches bis in die heutige Zeit hineinreicht. Es ist jedoch unklar, ob der Satz des Pythagoras wirklich auf Pythagoras von Samos zurückgeht, da alle Quellen über Pythagoras von Samos aus der Zeit nach seinem Wirken stammen und diese sich zum Teil sogar widersprechen. <ref>https://de.bettermarks.com/mathe/pythagoras-von-samos/ </ref> | |||
== Mathematische Aussage == | == Mathematische Aussage == | ||
| Zeile 12: | Zeile 12: | ||
Formal wird der Satz in Symbolsprache wie folgt formuliert: | Formal wird der Satz in Symbolsprache wie folgt formuliert: | ||
[[Datei:Satz des Pythagoras.jpg|mini| Visualisierung des Satz des Pythagoras]] | |||
[[Datei:Formel.jpg|100px]] | [[Datei:Formel.jpg|100px]] | ||
[[Datei:Satz des Pythagoras GIF.gif]] | |||
== Mathematische Anwendung == | == Mathematische Anwendung == | ||
Der Satz des Pythagoras findet in vielen Bereichen Anwendung. Einige davon sind im Folgenden aufgelistet. | |||
=== Längen im rechtwinkligen Dreieck === | === Längen im rechtwinkligen Dreieck === | ||
Die wohl häufigste Anwendung des Satz des Pythagoras im Schulkontext bildet die Berechnung der Seitenlängen in einem rechtiwnkligen Dreieck. Betrachte ein Dreieck wie im Bild rechts, in welchem die Seite c die Hypothenuse darstellt, dann lässt sich anhand zweier gegebener Seitenlängen mithilfe der folgenden Formeln, die sich unmittelbar aus dem Satz des Pythagoras ergeben, stets die fehlende dritte Seitenlänge berechnen. | |||
[[Datei:Formeln Berechnung.jpg|100px]] | |||
=== Euklidische Norm === | === Euklidische Norm === | ||
Das Prinzip des Satzes des Pythagoras kann auch verallgemeinert werden. So lässt sich beispielsweise mit folgender Formel die Raumdiagonale eines Quaderst berechnen. Diese erhält man durch zweimalige Anwendung des Satz des Pythagoras. | |||
[[Datei:Raumdiagonale.jpg|120px]] | |||
Führt man dieses Prinzip für höhere Dimensionen weiter fort, ergibt sich folgende Summenformel, die eine Norm auf dem n- dimensionalen reellen Raum bildet. | |||
[[Datei:Euklidische Norm.jpg|120px]] | |||
=== Pythagoreische Tripel === | === Pythagoreische Tripel === | ||
Pythagoreische Tripel sind ein Tripel reeller Zahlen a,b und c, für die der Satz des Pythagoras gilt, das heißt welche die [[Gleichung]] | |||
[[Datei:Formel.jpg|100px]] | |||
erfüllen. Diese lassen sich dabei mithilfe folgender Formeln erzeugen: | |||
[[Datei:Pythagoreische Tripel.jpg | 100px]] | |||
wobei x,y beliebige [[natürliche Zahlen]] mit x>y sind. <ref>https://de.wikipedia.org/wiki/Pythagoreisches_Tripel </ref>. | |||
Einige Beispiele für Pythagoreische Tripel sind: | |||
(3,4,5), (5,12,13), (15,8,17), (7,24,25), (35,12,37). | |||
== Beweise == | == Beweise == | ||
[[Datei:Beweis Satz des Pythagoras Bild.jpg|mini| Visualisierung des Beweises des Satz des Pythagoras]] | |||
Es gibt eine Vielzahl an [[Beweisen]] für den Satz des Pythagoras. Im Folgenden soll davon einer aufgeführt werden, welcher insbesondere im Schulkontext genutzt wird, um die Gültigkeit des Satz des Pythagoras zu zeigen. | |||
In ein Quadrat mit der Seitenlänge a+b werden vier kongruente rechtwinklige Dreiecke mit den Seiten a,b und c (Hypotenuse) entsprechend der Skizze eingelegt. Der Flächeninhalt des großen Quadrats beträgt nun | |||
[[Datei:Formel 2.jpg|70px]] | |||
Diesen erhalten wir ebenfalls, indem wir die Flächen der 4 [[kongruenten Dreiecke]] und den [[Flächeninhalt]] des inneren Quadrats mit der Seitenlänge c addieren. Dadurch erhalten wir die folgende Gleichung: | |||
[[Datei:Beweis Pythagoras.jpg|200px]] | |||
== Aufgabe == | |||
[[Datei:Bild Aufgabe Pythogoras.jpg|mini|Aufgabenvisualisierung]] | |||
Tom möchte seinen Fußball holen, der versehentlich beim Fußballspielen auf das Dach geflogen ist und jetzt in der Regenrinne festhängt. Dazu holt er eine 4,0 m lange Leiter und lehnt diese 1,5 m von der Hauswand entfernt an diese an. Bestimme, ob die Leiter bei dieser Entfernung zur Hauswand, bis zum Beginn des Daches zu einer Höhe von 3,50 m reicht und Tom damit seinen Fußball holen kann. | |||
== Literaturverzeichnis == | == Literaturverzeichnis == | ||
[[Kategorie: Mathematik]] [[Kategorie: Geometrie]] | |||
Aktuelle Version vom 31. Juli 2021, 18:49 Uhr
Der Satz des Pythagoras ist ein zentraler Satz der Geometrie. Er gilt als einer der am häufigsten bewiesenen Sätze der Mathematik. [1]
Geschichte
Der Satz des Pythagoras geht auf den griechischen Philosophen Pythagoras von Samos zurück, der von ca. 50 v. Chr. bis ca. 500 n. Chr. gelebt hat.[2] Pythagoras von Samos war ein griechischer Gelehrter und Philsoph und ist unter anderem noch für die nach ihm benannte Strömung der Pythagoreer bekannt. Der Satz des Pythagoras gilt dennoch als sein wichtigstes Erbe, welches bis in die heutige Zeit hineinreicht. Es ist jedoch unklar, ob der Satz des Pythagoras wirklich auf Pythagoras von Samos zurückgeht, da alle Quellen über Pythagoras von Samos aus der Zeit nach seinem Wirken stammen und diese sich zum Teil sogar widersprechen. [3]
Mathematische Aussage
Der Satz des Pythagoras beschreibt den Zusammenhang zwischen den Seitenlängen eines rechtwinkligen Dreiecks. Formal wird der Satz dabei wie folgt formuliert:
In einem rechtwinkligen Dreieck ist der Flächeninhalt des Quadrats über der Hypotenuse gleich der Summe der Flächeninhalte der Quadrate über den Katheten.
Formal wird der Satz in Symbolsprache wie folgt formuliert:

Mathematische Anwendung
Der Satz des Pythagoras findet in vielen Bereichen Anwendung. Einige davon sind im Folgenden aufgelistet.
Längen im rechtwinkligen Dreieck
Die wohl häufigste Anwendung des Satz des Pythagoras im Schulkontext bildet die Berechnung der Seitenlängen in einem rechtiwnkligen Dreieck. Betrachte ein Dreieck wie im Bild rechts, in welchem die Seite c die Hypothenuse darstellt, dann lässt sich anhand zweier gegebener Seitenlängen mithilfe der folgenden Formeln, die sich unmittelbar aus dem Satz des Pythagoras ergeben, stets die fehlende dritte Seitenlänge berechnen.
Euklidische Norm
Das Prinzip des Satzes des Pythagoras kann auch verallgemeinert werden. So lässt sich beispielsweise mit folgender Formel die Raumdiagonale eines Quaderst berechnen. Diese erhält man durch zweimalige Anwendung des Satz des Pythagoras.
Führt man dieses Prinzip für höhere Dimensionen weiter fort, ergibt sich folgende Summenformel, die eine Norm auf dem n- dimensionalen reellen Raum bildet.
Pythagoreische Tripel
Pythagoreische Tripel sind ein Tripel reeller Zahlen a,b und c, für die der Satz des Pythagoras gilt, das heißt welche die Gleichung
erfüllen. Diese lassen sich dabei mithilfe folgender Formeln erzeugen:
wobei x,y beliebige natürliche Zahlen mit x>y sind. [4].
Einige Beispiele für Pythagoreische Tripel sind:
(3,4,5), (5,12,13), (15,8,17), (7,24,25), (35,12,37).
Beweise
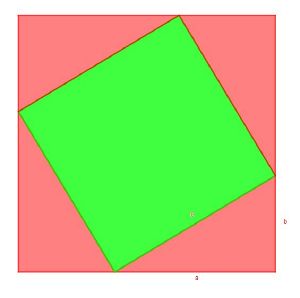
Es gibt eine Vielzahl an Beweisen für den Satz des Pythagoras. Im Folgenden soll davon einer aufgeführt werden, welcher insbesondere im Schulkontext genutzt wird, um die Gültigkeit des Satz des Pythagoras zu zeigen.
In ein Quadrat mit der Seitenlänge a+b werden vier kongruente rechtwinklige Dreiecke mit den Seiten a,b und c (Hypotenuse) entsprechend der Skizze eingelegt. Der Flächeninhalt des großen Quadrats beträgt nun
![]() Diesen erhalten wir ebenfalls, indem wir die Flächen der 4 kongruenten Dreiecke und den Flächeninhalt des inneren Quadrats mit der Seitenlänge c addieren. Dadurch erhalten wir die folgende Gleichung:
Diesen erhalten wir ebenfalls, indem wir die Flächen der 4 kongruenten Dreiecke und den Flächeninhalt des inneren Quadrats mit der Seitenlänge c addieren. Dadurch erhalten wir die folgende Gleichung:
Aufgabe
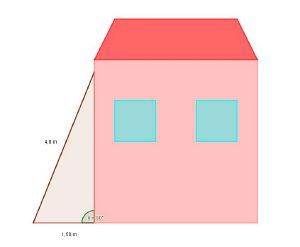
Tom möchte seinen Fußball holen, der versehentlich beim Fußballspielen auf das Dach geflogen ist und jetzt in der Regenrinne festhängt. Dazu holt er eine 4,0 m lange Leiter und lehnt diese 1,5 m von der Hauswand entfernt an diese an. Bestimme, ob die Leiter bei dieser Entfernung zur Hauswand, bis zum Beginn des Daches zu einer Höhe von 3,50 m reicht und Tom damit seinen Fußball holen kann.
Literaturverzeichnis
- ↑ Eli Maor: The Pythagorean Theorem: A 4,000-year History. Princeton University Press, Princeton 2007, ISBN 0-691-12526-0., S. XIII (Vorwort).
- ↑ https://de.bettermarks.com/mathe/pythagoras-von-samos/
- ↑ https://de.bettermarks.com/mathe/pythagoras-von-samos/
- ↑ https://de.wikipedia.org/wiki/Pythagoreisches_Tripel