Winkel: Unterschied zwischen den Versionen
DiMedS (Diskussion | Beiträge) |
DiMedS (Diskussion | Beiträge) |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Kategorie: Geometrie]] | |||
== Winkel == | == Winkel == | ||
| Zeile 84: | Zeile 85: | ||
=== Übung === | === Übung === | ||
Zeichne folgende Winkel (nutze dafür dein Geodreieck) und benenne | Zeichne folgende Winkel (nutze dafür dein Geodreieck) und benenne ihre Winkelart! | ||
a) 47° | a) 𝛼=47° | ||
b) 271° | b) 𝛽=271° | ||
c) 89° | c) 𝛾=89° | ||
d) 305° | d) 𝛿=305° | ||
=== Quellen === | === Quellen === | ||
Aktuelle Version vom 28. Juli 2021, 18:56 Uhr
Winkel
Zu den wichtigsten geometrischen Grundlagen gehören neben Punkt, Gerade, Strahl und Strecke auch die Winkel. Mithilfe dieser kann man die oben genannten geometrische Bausteine zu Figuren (Ebene Figuren) zusammensetzten, wie zum Beispiel: Vierecke oder Dreiecke.
An sich zwei schneidenden Geraden findet man Winkel mit besonderen Eigenschaften, z.B. Nebenwinkel und Scheitelwinkel.
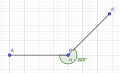
Eigenschaften
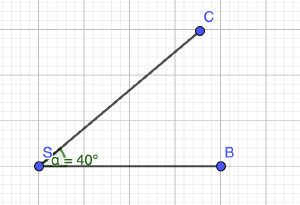
Zwei Strahlen g und h mit einem gemeinsamen Anfangspunkt schließen zusammen einen Winkel 𝛼 ein. Der Anfangspunkt S wird auch Scheitelpunkt genannt.
Bezeichnungen von Winkeln
a) Mithilfe von 3 Punkten, z.B. ∡BSC
b) Mithilfe von griechischen Buchstaben 𝛼: Alpha 𝛽: Beta 𝛾: Gamma 𝛿: Delta
Winkelarten
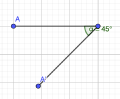
(1) Der Spitze Winkel: ist stets kleiner als 90°. Größe: 𝛼<90° Beispiel: 𝛼=45°
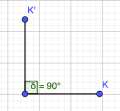
(2) Der Rechter Winkel: ist stets 90° groß. Größe: 𝛼 =90°
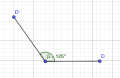
(3) Der Stumpfe Winkel: ist stets größer als 90° und kleiner als 180°. Größe: 90°<𝛼<180° Beispiel: 𝛼=125°
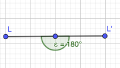
(4) Der Gestreckte Winkel: ist stets 180° groß. Größe: 𝛼=180°
(5) Der Überstumpfe Winkel: ist stets größer als 180° und kleiner als 360°. Größe: 180°< 𝛼<360° Beispiel: 𝛼=275°
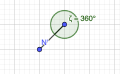
(6) Der Vollwinkel (auch Kreis genannt): ist stets 360° groß. Größe: 𝛼 =360°
(7) Der Nullwinkel: ist stets 0° groß. Größe: 𝛼=0°
Beispiele
-
Spitzer Winkel
-
Rechter Winkel
-
Stumpfer Winkel
-
Gestreckte Winkel
-
Überstumpfer Winkel
-
Vollwinkel/ Kreis
Winkel zeichnen
1. Lege den Scheitelpunkt S fest und zeichne den ersten Schenkel.
2. Lege die 0 des Geodreiecks an den Scheitelpunkt S und auf den ersten Schenkel an.
3. Wahl der Skala auf dem Geodreieck, an der du den Winkel abmisst.
(a) Der Scheitelpunkt liegt auf der linken Seite des Schenkels: der Winkel öffnet sich nach rechts. Lies den Wert des Winkels auf der oberen Skala des Geodreiecks ab und markiere ihn.
(b) Der Scheitelpunkt liegt auf der rechten Seite des Schenkels: der Winkel öffnet sich nach links. Lies den Wert des Winkels auf der unteren Skala des Geodreiecks ab und markiere ihn.
4. Zeichne den zweiten Schenkel des Winkels, indem du deinen markierten Punkt mit dem Scheitelpunkt S verbindest.
5. Ist der zu zeichnende Winkel ein überstumpfer Winkel (180°<𝜶<360°), musst du diesen Winkel in 2 Teile aufteilen, beispielsweise 𝜶=210°
(a) Ermittle die Differenz zwischen dem zu zeichnenden Winkel und 180°: 210° - 180° = 30°
(b) Zeichne den ersten Schenkel des Winkels. Setze nun eine Markierung bei 180°. Diese hilft dir später die korrekte Winkelgröße zu zeichnen.
(c) Drehe nun dein Geodreieck und miss die Gradzahl der vorher ermittelten Differenz ab. Achte dabei darauf den gestreckten Winkel weiterzuführen. Setze eine zweite Markierung, im Beispiel: 30°
(d) Verbinde die nun die zuletzt gesetzte Markierung mit dem Scheitelpunkt. Achte darauf beim Zeichnen deines Winkels die Markierung des gestreckten Winkels zu überschreiten.
Übung
Zeichne folgende Winkel (nutze dafür dein Geodreieck) und benenne ihre Winkelart!
a) 𝛼=47°
b) 𝛽=271°
c) 𝛾=89°
d) 𝛿=305°
Quellen
- ↑ Dennis Rudolph (2017). Geometrie: Geodreieck und Winkel. Online im Internet. URL: https://www.frustfrei-lernen.de/mathematik/geometrie-geodreieck-winkel-90-grad.html [27.07.2021]
- ↑ Dennis Rudolph (2017). Winkelarten. Online im Internet. URL: https://www.frustfrei-lernen.de/mathematik/winkeltypen-winkelarten.html [27.07.2021]