Seitenhalbierende: Unterschied zwischen den Versionen
DiMedS (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
DiMedS (Diskussion | Beiträge) |
||
| (8 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Die Seitenhalbierende ist eine [[Gerade]], die durch einen der Eckpunkte des Dreiecks und den [[Mittelpunkt]] der gegenüberliegenden [[Seite]] verläuft. Sie gehört wie die [[Mittelsenkrechte]] und [[Winkelhalbierende]] zu den besonderen [[Linien im Dreieck]]. | Die Seitenhalbierende ist eine [[Gerade]], die durch einen der Eckpunkte des Dreiecks und den [[Mittelpunkt]] der gegenüberliegenden [[Seite]] verläuft. Sie gehört wie die [[Mittelsenkrechte]], [[Höhe]] und [[Winkelhalbierende]] zu den besonderen [[Linien im Dreieck]]. | ||
[[Datei:Dreieck mit einer Seitenhalbierenden.png|mini|Das Dreieck ABC und dessen Seitenhalbierende s<sub>c</sub>]] | |||
= Definition = | = Definition = | ||
Eine Seitenhalbierende ist eine [[Gerade]] die durch den Eckpunkt eines Dreiecks und durch den [[Mittelpunkt]] der gegenüberliegenden Seite verläuft.<ref>vgl. Alsina, C. & Nelsen R.B. (2015): Perlen der Mathematik. Springer-Verlag Berlin Heidelberg. S.63.</ref> | |||
=Eigenschaften= | =Eigenschaften= | ||
Seitenhalbierende sind schon seit Jahrhunderten Thema mathematischer Untersuchungen. Vor allem der italienische Mathematiker [[Giovanni Ceva]] forschte viel zu ihnen. Ebenso wie die [[ | Seitenhalbierende sind schon seit Jahrhunderten Thema mathematischer Untersuchungen. Vor allem der italienische Mathematiker [[Giovanni Ceva]] forschte viel zu ihnen. Ebenso wie die [[Winkelhalbierende]]n und [[Höhe]]n im Dreieck werden die Seitenhalbierenden daher als [[Cevanen]] bezeichnet.<ref>vgl. Alsina, C. & Nelsen R.B. (2015): Perlen der Mathematik. Springer-Verlag Berlin Heidelberg. S.59.</ref> | ||
==Bezeichnung der Seitenhalbierenden== | ==Bezeichnung der Seitenhalbierenden== | ||
Die Seitenhalbierenden werden entsprechend ihres Schnittpunktes mit einem Eckpunkt des Dreiecks bezeichnet. Für das allgemeine Dreieck ABC gilt also 𝑠<sub>𝑎</sub>,𝑠<sub>𝑏</sub> 𝑢𝑛𝑑 𝑠<sub>𝑐</sub>. | Die Seitenhalbierenden werden entsprechend ihres Schnittpunktes mit einem Eckpunkt des Dreiecks bezeichnet. Für das allgemeine Dreieck ABC gilt also 𝑠<sub>𝑎</sub>, 𝑠<sub>𝑏</sub> 𝑢𝑛𝑑 𝑠<sub>𝑐</sub>. <ref>vgl. Alsina, C. & Nelsen R.B. (2015): Perlen der Mathematik. Springer-Verlag Berlin Heidelberg. S.63.</ref> | ||
[[Datei:Dreieck mit Seitenhalbierenden.png|mini|Dreieck mit Seitenhalbierenden]] | |||
==Teilung der Seiten== | ==Teilung der Seiten== | ||
Für die Seiten des Dreiecks gelten außerdem die folgenden | Für die Seiten des Dreiecks gelten außerdem die folgenden Verhältnisse <br> | ||
* 𝑎<sub>𝑏</sub> = 𝑎<sub>𝑐</sub> = 𝑎/''2'', <br> | |||
* 𝑏<sub>𝑎</sub> = 𝑏<sub>𝑐</sub> = 𝑏/''2'' und <br> | |||
* 𝑐<sub>𝑎</sub> = 𝑐<sub>𝑏</sub> = 𝑐/''2''. <ref>vgl. Alsina, C. & Nelsen R.B. (2015): Perlen der Mathematik. Springer-Verlag Berlin Heidelberg. S.63.</ref> | |||
==Schnittpunkt der Seitenhalbierenden== | ==Schnittpunkt der Seitenhalbierenden== | ||
Die Seitenhalbierenden schneiden sich in einem [[Schnittpunkt]]. Dieser wird auch als Schwerpunkt des Dreiecks mit dem Großbuchstaben G bezeichnet. Er unterteilt die Seitenhalbierenden im Verhältnis 2:1. | Die Seitenhalbierenden schneiden sich in einem [[Schnittpunkt]]. Dieser wird auch als '''Schwerpunkt des Dreiecks''' mit dem Großbuchstaben '''''G''''' bezeichnet. Er unterteilt die Seitenhalbierenden im Verhältnis 2:1.<ref>vgl. Zeuge, W.(2018): Nützliche und schöne Geometrie. Springer-Verlag Berlin Heidelberg. S.59.</ref> | ||
==Teilung des Dreiecksfläche== | ==Teilung des Dreiecksfläche== | ||
Die drei Seitenhalbierenden 𝑠<sub>𝑎</sub>,𝑠<sub>𝑏</sub> 𝑢𝑛𝑑 𝑠<sub>𝑐</sub> unterteilen die Fläche des Dreiecks ABC in sechs gleichgroße Flächen. | Die drei Seitenhalbierenden 𝑠<sub>𝑎</sub>, 𝑠<sub>𝑏</sub> 𝑢𝑛𝑑 𝑠<sub>𝑐</sub> unterteilen die Fläche des Dreiecks ABC in sechs gleichgroße Flächen. | ||
[[Datei: Flächenaufteilung durch Seitenhalbierende.png|mini|Flächenaufteilung durch die Seitenhalbierenden]] | |||
(Beweis siehe Alsina & Nelsen 2015, S.64 <ref>vgl. Alsina, C & Nelsen R.B. (2015): Perlen der Mathematik. Springer-Verlag Berlin Heidelberg. S.64.</ref>) | |||
==Zusammenhang zwischen den Seitenhalbierenden und den Seiten des Dreiecks== | |||
Es gilt: <ref>vgl. Alsina, C & Nelsen R.B. (2015): Perlen der Mathematik. Springer-Verlag Berlin Heidelberg. S.63.</ref> | |||
* 𝑠<sub>𝑐</sub><sup>2</sup> = (𝑎<sup>2</sup> + 𝑏<sup>2</sup> )/2 − 𝑐<sup>2</sup>/4 | |||
* 𝑠<sub>𝑏</sub><sup>2</sup> = (𝑐<sup>2</sup> + 𝑎<sup>2</sup> )/2 − 𝑏<sup>2</sup>/4 | |||
* 𝑠<sub>𝑎</sub><sup>2</sup> = (𝑏<sup>2</sup> + 𝑐<sup>2</sup> )/2 − 𝑎<sup>2</sup>/4. | |||
Daraus folgt: 𝑠<sub>𝑎</sub><sup>2</sup> − 𝑠<sub>𝑏</sub><sup>2</sup> = (𝑏<sup>2</sup> + 𝑐<sup>2</sup>)/2 − 𝑎<sup>2</sup>/4 − (𝑐<sup>2</sup> + 𝑎<sup>2</sup>)/2 + 𝑏<sup>2</sup>/4 = 3/4 𝑏^<sup>2</sup> − 3/4 𝑎<sup>2</sup> = 3/4 (𝑏<sup>2</sup> − 𝑎<sup>2</sup>) | |||
Das bedeutet, falls a ≤ b ≤ c, so ist 𝑠<sub>𝑎</sub> ≥ 𝑠<sub>𝑏</sub> ≥ 𝑠<sub>𝑐</sub>. | |||
Außerdem gilt: 𝑠<sub>𝑎</sub><sup>2</sup> + 𝑠<sub>𝑏</sub><sup>2</sup> + 𝑠<sub>c</sub><sup>2</sup> = (𝑏<sup>2</sup> + 𝑐<sup>2</sup> )/2 − 𝑎<sup>2</sup>/4 +(𝑐<sup>2</sup> + 𝑎<sup>2</sup> )/2 + 𝑏<sup>2</sup>/4 + (𝑎<sup>2</sup> + 𝑏<sup>2</sup> )/2 − 𝑐<sup>2</sup>/4 = 3/4 𝑎<sup>2</sup> + 3/4 𝑏<sup>2</sup> + 3/4 𝑐<sup>2</sup> = 3/4 (𝑎<sup>2</sup> + 𝑏<sup>2</sup> + 𝑐<sup>2</sup>) | |||
=Konstruktion= | |||
Zur Konstruktion der Seitenhalbierenden mit Zirkel und Lineal ist es notwendig, ebenfalls [[Mittelsenkrechte]]n als Hilfslinien konstruieren zu können. | |||
# Schritt: Konstruiere die [[Mittelsenkrechte]] über einer Seite deiner Wahl. | |||
# Schritt: Bezeichne den Schnittpunkt der Seite mit der Mittelsenkrechte mit einem Großbuchstaben deiner Wahl. | |||
# Schritt: Verbinde den Schnittpunkt mit dem Eckpunkt des Dreiecks, der der Seite gegenüberliegt. | |||
# Schritt: Wiederhole das Vorgehen für die verbleibenden Seiten. | |||
# Schritt: Bezeichne den Schnittpunkt der Seitenhalbierenden mit ''G''. | |||
=Beispielaufgabe= | |||
==Aufgabenstellung== | |||
Zeichne das Dreieck ΔABC mit den vorgegebenen Punkten in ein Koordinatensystem (eine Längeneinheit entspricht einem Zentimeter). | |||
Bestimme den Schwerpunkt des Dreiecks sowie die Längen der Seitenhalbierenden 𝑠<sub>𝑎</sub>, 𝑠<sub>𝑏</sub> und 𝑠<sub>𝑐</sub>. | |||
A = ( 1 ; 1 ), B = ( 12 ; 3 ), C = ( 8 ; 11 ). | |||
''Hinweis:'' Beachte die angegebenen Koordinaten, um ein passendes Koordinatensystem zu wählen. | |||
==Lösung== | |||
[[Datei:Lösung Seitenhalbierende.png|mini|Zur Lösung der Aufgabe|left]] | |||
= | |||
=Quellen= | |||
[[Kategorie:Geometrie]] | |||
Aktuelle Version vom 2. September 2021, 10:45 Uhr
Die Seitenhalbierende ist eine Gerade, die durch einen der Eckpunkte des Dreiecks und den Mittelpunkt der gegenüberliegenden Seite verläuft. Sie gehört wie die Mittelsenkrechte, Höhe und Winkelhalbierende zu den besonderen Linien im Dreieck.
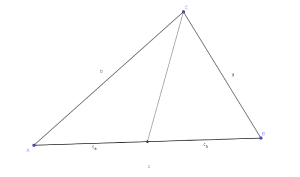
Definition
Eine Seitenhalbierende ist eine Gerade die durch den Eckpunkt eines Dreiecks und durch den Mittelpunkt der gegenüberliegenden Seite verläuft.[1]
Eigenschaften
Seitenhalbierende sind schon seit Jahrhunderten Thema mathematischer Untersuchungen. Vor allem der italienische Mathematiker Giovanni Ceva forschte viel zu ihnen. Ebenso wie die Winkelhalbierenden und Höhen im Dreieck werden die Seitenhalbierenden daher als Cevanen bezeichnet.[2]
Bezeichnung der Seitenhalbierenden
Die Seitenhalbierenden werden entsprechend ihres Schnittpunktes mit einem Eckpunkt des Dreiecks bezeichnet. Für das allgemeine Dreieck ABC gilt also 𝑠𝑎, 𝑠𝑏 𝑢𝑛𝑑 𝑠𝑐. [3]
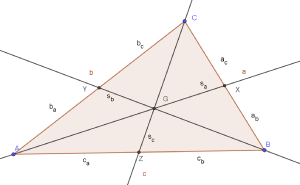
Teilung der Seiten
Für die Seiten des Dreiecks gelten außerdem die folgenden Verhältnisse
- 𝑎𝑏 = 𝑎𝑐 = 𝑎/2,
- 𝑏𝑎 = 𝑏𝑐 = 𝑏/2 und
- 𝑐𝑎 = 𝑐𝑏 = 𝑐/2. [4]
Schnittpunkt der Seitenhalbierenden
Die Seitenhalbierenden schneiden sich in einem Schnittpunkt. Dieser wird auch als Schwerpunkt des Dreiecks mit dem Großbuchstaben G bezeichnet. Er unterteilt die Seitenhalbierenden im Verhältnis 2:1.[5]
Teilung des Dreiecksfläche
Die drei Seitenhalbierenden 𝑠𝑎, 𝑠𝑏 𝑢𝑛𝑑 𝑠𝑐 unterteilen die Fläche des Dreiecks ABC in sechs gleichgroße Flächen.
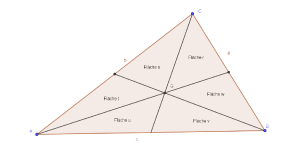
(Beweis siehe Alsina & Nelsen 2015, S.64 [6])
Zusammenhang zwischen den Seitenhalbierenden und den Seiten des Dreiecks
Es gilt: [7]
- 𝑠𝑐2 = (𝑎2 + 𝑏2 )/2 − 𝑐2/4
- 𝑠𝑏2 = (𝑐2 + 𝑎2 )/2 − 𝑏2/4
- 𝑠𝑎2 = (𝑏2 + 𝑐2 )/2 − 𝑎2/4.
Daraus folgt: 𝑠𝑎2 − 𝑠𝑏2 = (𝑏2 + 𝑐2)/2 − 𝑎2/4 − (𝑐2 + 𝑎2)/2 + 𝑏2/4 = 3/4 𝑏^2 − 3/4 𝑎2 = 3/4 (𝑏2 − 𝑎2)
Das bedeutet, falls a ≤ b ≤ c, so ist 𝑠𝑎 ≥ 𝑠𝑏 ≥ 𝑠𝑐.
Außerdem gilt: 𝑠𝑎2 + 𝑠𝑏2 + 𝑠c2 = (𝑏2 + 𝑐2 )/2 − 𝑎2/4 +(𝑐2 + 𝑎2 )/2 + 𝑏2/4 + (𝑎2 + 𝑏2 )/2 − 𝑐2/4 = 3/4 𝑎2 + 3/4 𝑏2 + 3/4 𝑐2 = 3/4 (𝑎2 + 𝑏2 + 𝑐2)
Konstruktion
Zur Konstruktion der Seitenhalbierenden mit Zirkel und Lineal ist es notwendig, ebenfalls Mittelsenkrechten als Hilfslinien konstruieren zu können.
- Schritt: Konstruiere die Mittelsenkrechte über einer Seite deiner Wahl.
- Schritt: Bezeichne den Schnittpunkt der Seite mit der Mittelsenkrechte mit einem Großbuchstaben deiner Wahl.
- Schritt: Verbinde den Schnittpunkt mit dem Eckpunkt des Dreiecks, der der Seite gegenüberliegt.
- Schritt: Wiederhole das Vorgehen für die verbleibenden Seiten.
- Schritt: Bezeichne den Schnittpunkt der Seitenhalbierenden mit G.
Beispielaufgabe
Aufgabenstellung
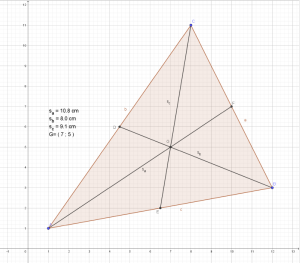
Zeichne das Dreieck ΔABC mit den vorgegebenen Punkten in ein Koordinatensystem (eine Längeneinheit entspricht einem Zentimeter). Bestimme den Schwerpunkt des Dreiecks sowie die Längen der Seitenhalbierenden 𝑠𝑎, 𝑠𝑏 und 𝑠𝑐.
A = ( 1 ; 1 ), B = ( 12 ; 3 ), C = ( 8 ; 11 ).
Hinweis: Beachte die angegebenen Koordinaten, um ein passendes Koordinatensystem zu wählen.
Lösung
Quellen
- ↑ vgl. Alsina, C. & Nelsen R.B. (2015): Perlen der Mathematik. Springer-Verlag Berlin Heidelberg. S.63.
- ↑ vgl. Alsina, C. & Nelsen R.B. (2015): Perlen der Mathematik. Springer-Verlag Berlin Heidelberg. S.59.
- ↑ vgl. Alsina, C. & Nelsen R.B. (2015): Perlen der Mathematik. Springer-Verlag Berlin Heidelberg. S.63.
- ↑ vgl. Alsina, C. & Nelsen R.B. (2015): Perlen der Mathematik. Springer-Verlag Berlin Heidelberg. S.63.
- ↑ vgl. Zeuge, W.(2018): Nützliche und schöne Geometrie. Springer-Verlag Berlin Heidelberg. S.59.
- ↑ vgl. Alsina, C & Nelsen R.B. (2015): Perlen der Mathematik. Springer-Verlag Berlin Heidelberg. S.64.
- ↑ vgl. Alsina, C & Nelsen R.B. (2015): Perlen der Mathematik. Springer-Verlag Berlin Heidelberg. S.63.