Figuren: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 5: | Zeile 5: | ||
Im [[Lehrplan]] Sachsen Klassenstufe 1 & 2 müssen Schülerinnen und Schüler folgende [[ebene Figuren]] kennen: | Im [[Lehrplan]] Sachsen Klassenstufe 1 & 2 müssen Schülerinnen und Schüler folgende [[ebene Figuren]] kennen: | ||
=== Dreieck === | === Arten=== | ||
==== Dreieck ==== | |||
[[Datei:Dreieck.png|mini|Beispielbild Dreieck]] | [[Datei:Dreieck.png|mini|Beispielbild Dreieck]] | ||
Ein Dreieck ist eine [[ebene Figur]] und besteht aus drei [[Strecken]], von denen je zwei Seiten einen gemeinsamen [[Eckpunkt]] haben. | Ein Dreieck ist eine [[ebene Figur]] und besteht aus drei [[Strecken]], von denen je zwei Seiten einen gemeinsamen [[Eckpunkt]] haben. | ||
| Zeile 16: | Zeile 17: | ||
=== Viereck === | ==== Viereck ==== | ||
Ein [[Viereck]] ist eine [[ebene Figur]] und besteht aus vier [[Seiten]] und vier [[Ecken]]. | Ein [[Viereck]] ist eine [[ebene Figur]] und besteht aus vier [[Seiten]] und vier [[Ecken]]. | ||
==== Rechteck ==== | ===== Rechteck ===== | ||
[[Datei:Rechteck.png|mini|Beispielbild Rechteck]] | [[Datei:Rechteck.png|mini|Beispielbild Rechteck]] | ||
| Zeile 42: | Zeile 43: | ||
==== Quadrat ==== | ===== Quadrat ===== | ||
[[Datei:Quadrat.png|mini|Beispielbild Quadrat]] | [[Datei:Quadrat.png|mini|Beispielbild Quadrat]] | ||
Version vom 20. Januar 2020, 20:37 Uhr
Figur (lat. figura: Gebilde, Gestalt) ist ein Begriff, der in vielen Themengebieten aufgegriffen wird, wie beispielsweise Kunstfigur, Werbefigur, literarische Figur etc. und verschiedene Bedeutungen einnehmen kann. In der Mathematik wird von einer sog. Geometrischen Figur gesprochen. In der Grundschulmathematik spielt dabei vorrangig die Themengebiete der ebenen Figuren und linearen Figuren eine wichtige Rolle im Lernbereich der Geometrie.
Ebene Figuren
Im Lehrplan Sachsen Klassenstufe 1 & 2 müssen Schülerinnen und Schüler folgende ebene Figuren kennen:
Arten
Dreieck
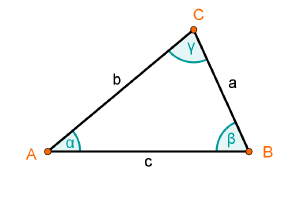
Ein Dreieck ist eine ebene Figur und besteht aus drei Strecken, von denen je zwei Seiten einen gemeinsamen Eckpunkt haben.
Eigenschaften:
- Ein Dreieck hat drei Seiten, die meistens mit a, b und c bezeichnet werden.
- Die Eckpunkte hingegen werden oft mit A, B und C gekennzeichnet.
- Es entstehen drei Winkel im Dreieck, die meistens Alpha, Beta und Gamma genannt werden.
- Die Summe dieser drei Winkel - auch Innenwinkel genannt - beträgt 180 Grad.
Viereck
Ein Viereck ist eine ebene Figur und besteht aus vier Seiten und vier Ecken.
Rechteck
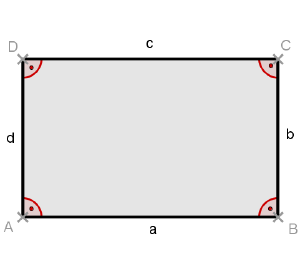
Eigenschaften:
- Ein Rechteck hat 4 Ecken.
- Alle Innenwinkel sind gleich groß und betragen 90 Grad (rechter Winkel).
- Die gegenüberliegenden Seiten sind gleich lang und parallel zueinander.
- Die Diagonalen eines Rechtecks sind gleich lang und halbieren einander.
Quadrat
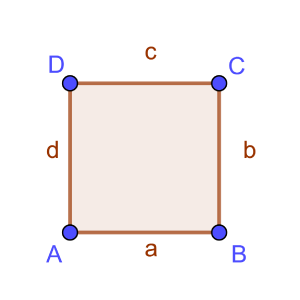
Eigenschaften:
- Ein Quadrat hat 4 Ecken.
- Alle Innenwinkel sind gleich groß und betragen 90 Grad (rechter Winkel).
- Alle Seiten sind gleich lang und parallel zueinander.
- Die Diagonalen stehen senkrecht aufeinander, sind gleich lang und halbieren einander.
Anwendung
Ebene Figuren können vielseitig eingesetzt werden, beispielsweise durch das Auslegen bzw. Nachlegen, Beschreiben oder selbstständige Erfinden von folgenden Elementen:

Zusammengesetzte Figuren
Bei Zusammengesetzte Figuren werden ebene Figuren miteinander kombiniert, sodass eine neue Fläche entsteht.
Tangrams
Ein Tangram ist eine spezielle zusammengesetzte Figur, die durch eine feste Kobination von ebenen Figuren definiert ist, welche jedoch beliebig zusammengesetzt werden können. Das originale Tangram besteht aus 7 ebenen Figuren, die zusammen ein [[[Quadrat]] bilden: Zwei große Dreiecke], ein mittelgrosses Dreieck, zwei kleine Dreiecke, ein Quadrat und ein Parallelogramm. Für die Neubildung einer zusammengesetzten Figur müssen alle sieben Steine verwendet werden.
Muster
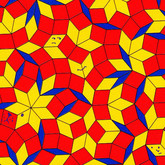
Ein Muster bezeichnet allgemein eine Struktur, die durch eine gleichförmige Wiederholung verwendeter Elemente gekennzeichnet ist. Hierbei können in der Grundschule auch Bezüge zur ästhetischen Kunst hergestellt werden.