Kongruenz: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 5: | Zeile 5: | ||
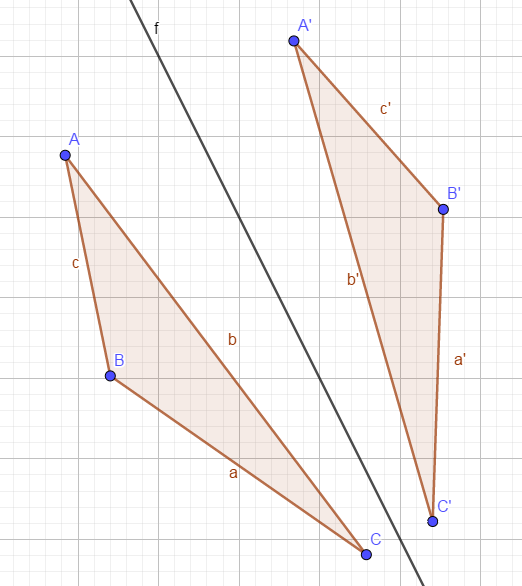
Es gibt 4 Kongruenzsätze für [[Dreiecke]]. Sie sind nicht nur wichtig, um zu überprüfen, ob Kongruenz vorliegt. Sie spielen auch eine bedeutende Rolle für das [[Konstruieren]] von [[Dreiecken]]. | Es gibt 4 Kongruenzsätze für [[Dreiecke]]. Sie sind nicht nur wichtig, um zu überprüfen, ob Kongruenz vorliegt. Sie spielen auch eine bedeutende Rolle für das [[Konstruieren]] von [[Dreiecken]]. | ||
[[Datei:Kongruenz.png]] | |||
===Kongruenzsatz SSS=== | ===Kongruenzsatz SSS=== | ||
Version vom 30. Juli 2020, 15:41 Uhr
Als Kongruenz bezeichnet man die Deckungsgleichheit zweier Figuren. Zueinander kongruente Figuren haben also denselben Flächeninhalt. Besonders wichtig ist diese Eigenschaft bei Dreiecken. Denn man kann überprüfen, ob zwei Dreiecke zueinander kongruent sind, wenn man bestimmte Eigenschaften von ihnen kennt. Das drücken die sogenannten Kongruenzsätze aus. Sind zwei Dreiecke kongruent, schreibt man Die Kongruenz ist ein Spezialfall der Ähnlichkeit.
Die Kongruenzsätze für Dreiecke
Es gibt 4 Kongruenzsätze für Dreiecke. Sie sind nicht nur wichtig, um zu überprüfen, ob Kongruenz vorliegt. Sie spielen auch eine bedeutende Rolle für das Konstruieren von Dreiecken.
Kongruenzsatz SSS
Zwei Dreiecke sind zueinander kongruent, wenn sie in der Länge aller drei Seiten übereinstimmen.
Kongruenzsatz SWS
Zwei Dreiecke sind zueinander kongruent, wenn sie in der Länge zweier Seiten und im von diesen eingeschlossenen Winkel übereinstimmen.
Kongruenzsatz WSW
Zwei Dreiecke sind zueinander kongruent, wenn sie in einer Seite und den beiden anliegenden Winkeln übereinstimmen.
Kongruenzsatz SSW
Zwei Dreiecke sind zueinander kongruent, wenn sie in zwei Seiten und dem der größeren Seite gegenüberliegenden Winkel übereinstimmen.
Übungsaufgaben
1. Begründe, warum es keinen Kongruenzsatz WWW für Dreiecke gibt. 2.