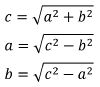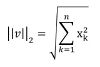Satz des Pythagoras

Der Satz des Pythagoras ist ein zentraler Satz der Geometrie. Er gilt als einer der am häufigsten bewiesenen Sätze der Mathematik.

Mathematische Aussage

Der Satz des Pythagoras beschreibt den Zusammenhang zwischen den Seitenlängen eines rechtwinkligen Dreiecks. Formal wird der Satz dabei wie folgt formuliert:

In einem rechtwinkligen Dreieck ist der Flächeninhalt des Quadrats über der Hypotenuse gleich der Summe der Flächeninhalte der Quadrate über den Katheten.

Formal wird der Satz in Symbolsprache wie folgt formuliert:

Visualisierung des Satz des Pythagoras

Mathematische Anwendung

Der Satz des Pythagoras findet in vielen Bereichen Anwendung. Einige davon sind im Folgenden aufgelistet.

Längen im rechtwinkligen Dreieck

Die wohl häufigste Anwendung des Satz des Pythagoras im Schulkontext bildet die Berechnung der Seitenlängen in einem rechtiwnkligen Dreieck. Betrachte ein Dreieck wie im Bild rechts, in welchem die Seite c die Hypothenuse darstellt, dann lässt sich anhand zweier gegebener Seitenlängen mithilfe der folgenden Formeln, die sich unmittelbar aus dem Satz des Pythagoras ergeben, stets die fehlende dritte Seitenlänge berechnen.

Euklidische Norm

Das Prinzip des Satzes des Pythagoras kann auch verallgemeinert werden. So lässt sich beispielsweise mit folgender Formel die Raumdiagonale eines Quaderst berechnen. Diese erhält man durch zweimalige Anwendung des Satz des Pythagoras.

Führt man dieses Prinzip für höhere Dimensionen weiter fort, ergibt sich folgende Summenformel, die eine Norm auf dem n- dimensionalen reellen Raum bildet.