Drachenviereck

Drachenviereck

Ein Drachenviereck ist geometrische Figur. Es handelt sich hierbei genauer um ein Viereck, bei dem jeweils zwei aneinandergrenzende Seiten gleich lang sind. Die Diagonalen, wovon eine die Symmetrieachse darstellt, stehen in einem Drachenviereck senkrecht aufeinander.

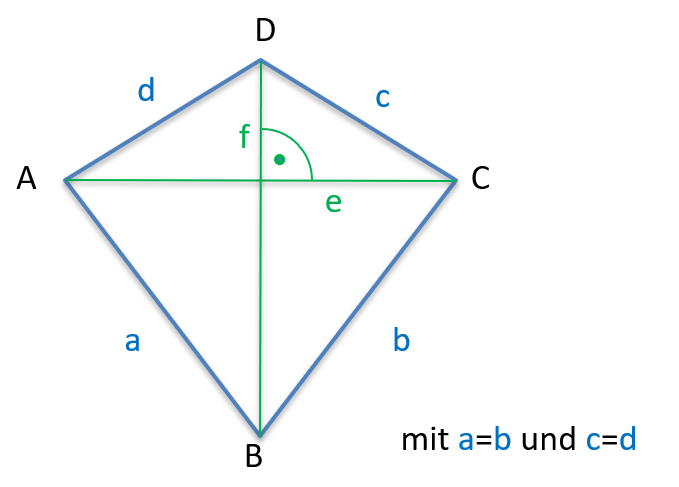
Beschriftung des Drachenvierecks

Besondere Eigenschaften des Drachenvierecks

- Ein Drachenviereck entsteht, wenn man ein beliebiges Dreieck an einer der Dreiecksseiten spiegelt.

- Mindestens zwei gegenüberliegende Winkel sind gleich groß.

- Ein Drachenviereck ist immer achsensymmetrisch. Die Symmetrieachse ist hierbei stets eine der beiden Diagonalen.

- Ein Drachenviereck ist i.d.R nicht punktsymmetrisch.

- Ein Drachenviereck mit vier gleich langen Seiten (a=b=c=d), ist eine Raute.

- Ein Drachenviereck mit vier rechten Winkeln und vier gleich langen Seiten, ist ein Quadrat.

Berechnungen am Drachenviereck

Umfang

Der Umfang eines Drachenvierecks ergibt sich aus der Summe der Seitenlängen. Hierbei sind zwei Seiten stets gleich lang, so dass gilt: u = 2(a+c)

Flächeninhalt

Der Flächeninhalt eines Drachenvierecks ergibt sich aus der Hälfte des Produkts der beiden Diagonalen: A = (ef)/2

Übungsaufgabe

Vervollständige die fehlenden Werte und konstruiere das folgende Drachenviereck. Berechne anschließend Umfang und Flächeninhalt. a = 2 cm d = 5 cm e = 8 cm

Quellen

https://www.lernhelfer.de/schuelerlexikon/mathematik/artikel/drachenviereck https://de.serlo.org/mathe/1733/drachenviereck