Schriftliche Division

Die schriftliche Division ist eine Form der Division. Sie hilft dir beim Dividieren großer Zahlen. Gerade bei Divisionsaufgaben, wo der Dividend über das kleine Einmaleins hinausgeht, ist die schriftliche Division sehr hilfreich. Die Wiederholung der Grundbegriffe der Division findest du unter Division.

In diesem Artikel wird dir die schriftliche Division ohne Rest erklärt.

Schaue auch mal hier nach: Schriftliche Division mit Dezimalzahlen, Schriftliche Division mit Rest

Voraussetzungen

Die Voraussetzung für die schriftliche Subtraktion sind das Beherrschen:

• der schriftlichen Subtraktion
• des Einmaleins

Schritt für Schritt erklärt

1. Aufgabe aufschreiben

Zuerst schreibst du die Aufgabe zum Beispiel in dein Übungsheft.

2. Erste Division

• 1. Schritt:
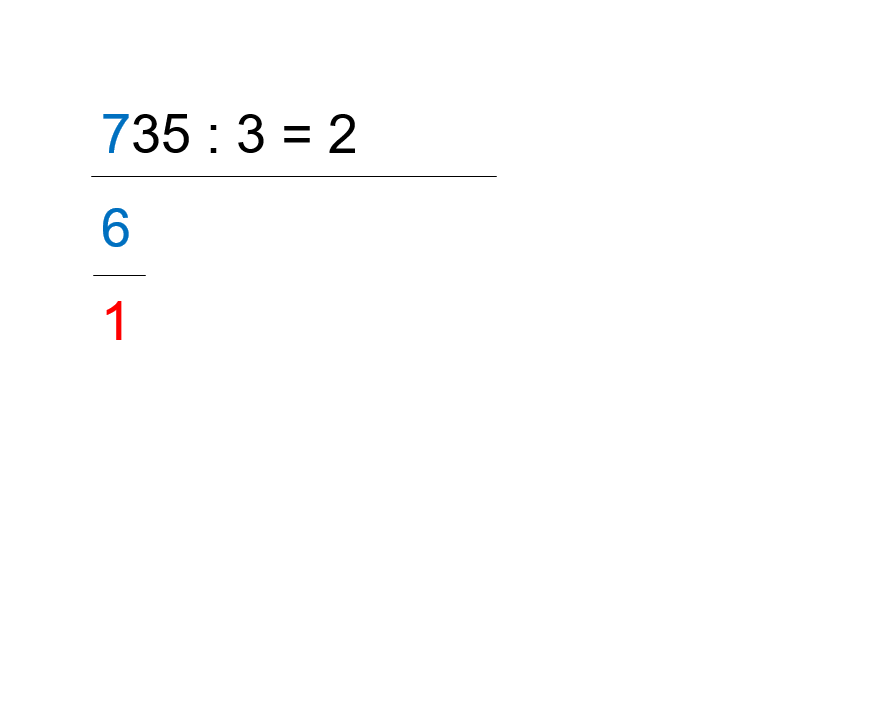
  • Betrachte die erste Zahl des Dividenden. Wie oft passt die 3 in die 7?
  • Die Antwort lautet: 2 Mal.
  • Die 2 wird nun rechts neben das Gleichheitszeichen geschrieben.

• 2. Schritt
  • Nun wird überprüft, ob bei der Division ein Rest übrig bleibt.
  • Wir rechnen zunächst: 2·3=6
  • Die 6 schreiben wir unter die erste Zahl des Dividenden.

• 3. Schritt
  • Nun ziehen wir von der ersten Zahl des Dividenden die eben berechnete Zahl 6 ab.
  • Wir rechnen deshalb: 7-6=1
  • Die 1 ist dabei der Rest der ersten Division.

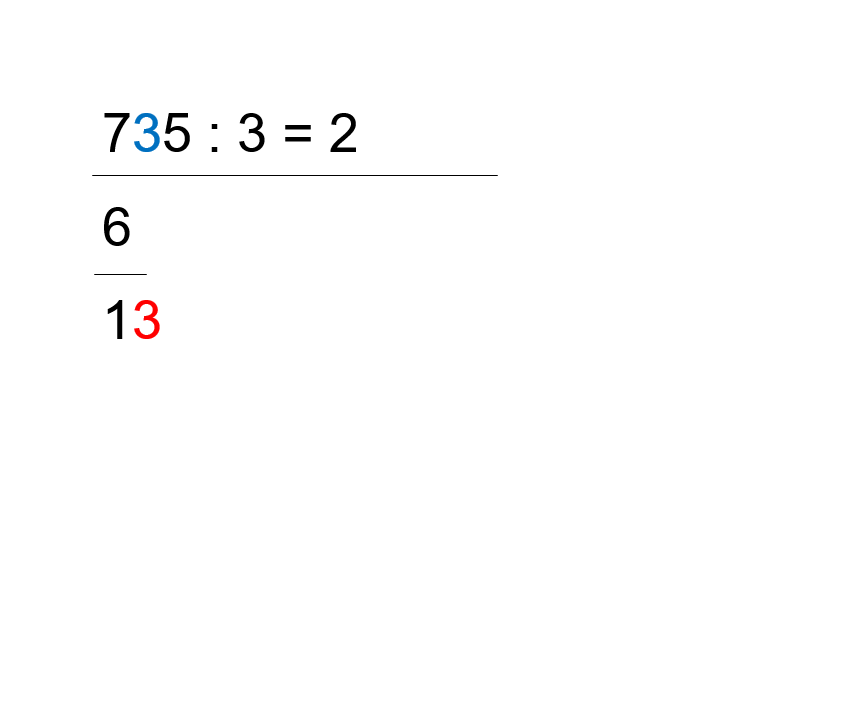
• 4. Schritt
  • Zum Abschluss der ersten Division holen wir die zweite Zahl des Dividenden (die 3) herunter in die letzte Zeile.
  • Wir schreiben also die 3 der blauen Stelle an die rote Stelle.

2. Division

• 1. Schritt
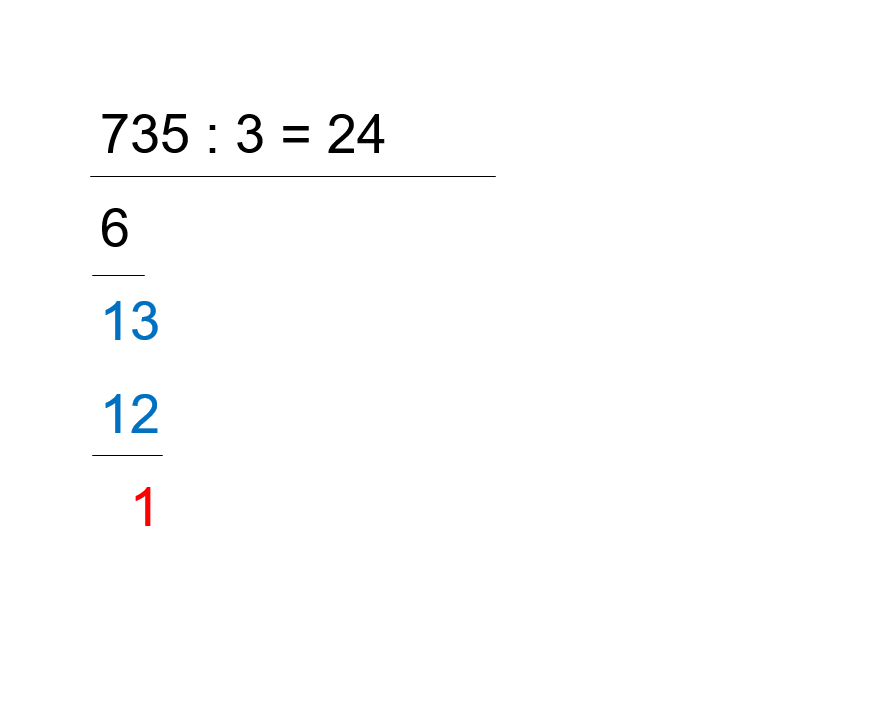
  • Wie oft passt die 3 in die 13?
  • Die Antwort lautet: 4 Mal.
    • Die 4 notieren wir wieder rechts neben dem Gleichheitszeichen.

• 2. Schritt
  • Nun wird wieder geschaut, ob ein Rest vorhanden ist.
  • Dazu rechnen wir zunächst: 4·3=12
  • Die 12 schreiben wir nun in eine neue Zeile unter der 13.

• 3. Schritt
  • Wir rechnen nun: 13-12=1
  • Bei der zweiten Division bleibt also ein Rest von 1.

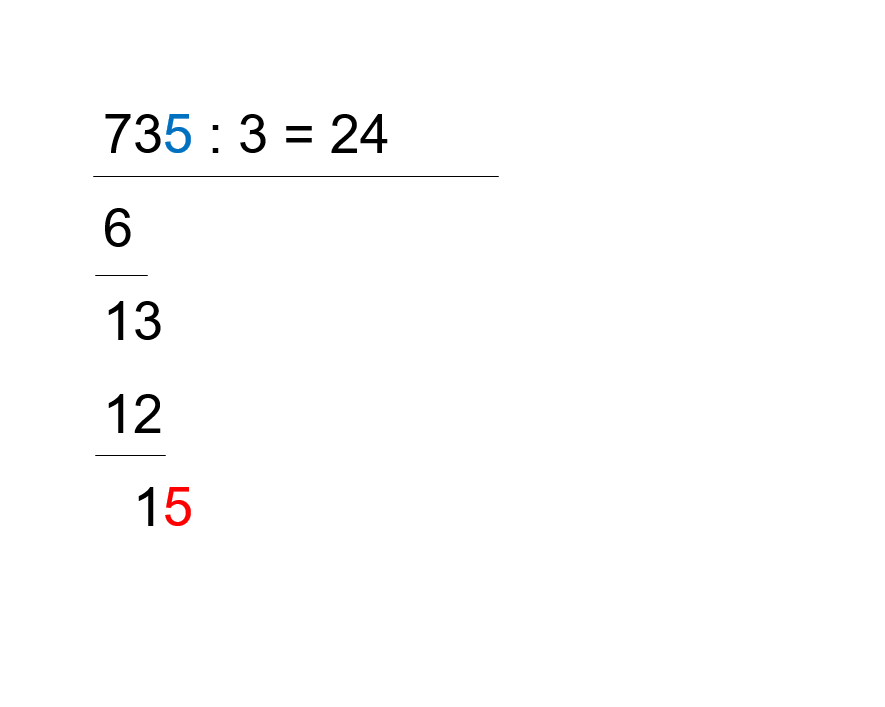
• 4. Schritt
  • Zum Abschluss der zweiten Division wird die dritte Zahl des Dividenden heruntergeholt und rechts neben die 1 geschrieben.

3. Division

• 1. Schritt
  • Wie oft passt die 3 in die 15?
  • Die Antwort lautet: 5 Mal.
  • Diese Zahl schreiben wir wieder rechts neben das Gleichheitszeichen.

• 2. Schritt
  • Nun überprüfen wir wieder, ob ein Rest bei der dritten Division vorhanden ist.
  • Dazu rechnen wir: 5·3=15
  • Die 15 schreiben wir in eine neue Zeile unter die bereits notierten 15.

• 3. Schritt
  • Wir rechnen nun 15-15=0
  • Die 0 sagt uns, dass bei dieser Division kein Rest mehr vorhanden ist.

• 4. Schritt
  • Da es keine weiteren Stellen beim Dividenden gibt, die wir herunterziehen müssen, entfällt dieser Schritt. Die Rechnung ist somit beendet.

4. Ergebnis ablesen

Die Zahl rechts neben dem Gleichheitszeichen ist das Ergebnis der Aufgabe und kann einfach abgelesen werden.

Übungsaufgaben

Rechne nun allein!

325 : 5 =

308 : 7 =

858 : 6 =

4329 : 9 =

Lösungen

325 : 5 = 65

308 : 7 = 44

858 : 6 = 143

4329 : 9 = 481