Quadrat

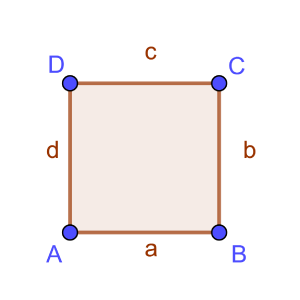
Ein Quadrat (lateinisch quadrum = Viereck) ist ein besonderes Viereck, bei welchem alle Seiten gleich lang und zueinander senkrecht sind.

Eigenschaften

Das Quadrat besitzt folgende Eigenschaften:

• Es besitzt 4 Ecken und 4 gleichlange Seiten (a=b=c=d)
• Alle Innenwinkel sind gleich groß (α=β=γ=δ)
• Gegenüberliegende Seiten sind parallel zueinander (a || c und b || d)
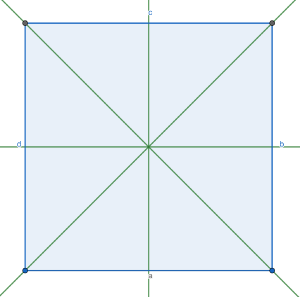
• Die Diagonalen sind gleich lang und zueinander senkrecht.
• Ein Quadrat besitzt 4 Symmetrieachsen.

Symmetrieachsen eines Quadrats

Betrachten wir die Stellung des Quadrats im Haus der Vierecke, so vereint es die Besonderheiten einer Raute mit denen eines Rechtecks.

Quadrat im Alltag

Um die Eigenschaften des Quadrats zu verdeutlichen, ist es ratsam, Objekte mit einer quadratischen Grundform zu betrachten. Beispiele im Alltag sind unter anderen:

• Verkehrsschilder (z.B. 30er Zone, Fußgängerüberweg)
• Schokoladentafeln von Rittersport
• Tafelflügel einer Kreidetafel (Achtung! Es gibt Tafel, deren Flügel rechteckig und nicht quadratisch sind)
• Schachbretter (und die Flächen eines Schachbretts)
• eine Seite eines Würfels
• Steckdosen und Lichtschalter
• Servietten
• Sofakissen (und einige Kopfkissen)

Außerdem ist ein quadratisches Blatt Papier die Ausgangsfigur der meisten Origami-Faltungen.

Berechnungen am Quadrat

So wie bei jeder ebenen Figur kann man auch bei einem Quadrat den Umfang und den Flächeninhalt berechnen.

Umfang

Da das Quadrat vier gleich lange Seiten besitzt, lässt sich der Umfang eines Quadrats mit der folgenden Formel berechnen: U=a+a+a+a bzw. U = 4∙a

Flächeninhalt

Um den Flächeninhalt eines Quadrats zu berechnen, lässt sich folgende Formel anwenden: A=a∙a bzw. A=a²

Übungsaufgabe

Gegeben ist ein Quadrat mit der Seitenlänge a=4cm. Berechne den Umfang und den Flächeninhalt.

Literatur

Rolles,G. & Unger, M. (Hrsg.) (2010): Basiswissen Schule Mathematik. 5. bis 10. Klasse. 4., neu bearbeitete Auflage. Berlin: Duden.