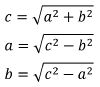Satz des Pythagoras: Unterschied zwischen den Versionen
DiMedS (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
DiMedS (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| Zeile 20: | Zeile 20: | ||
== Mathematische Anwendung == | == Mathematische Anwendung == | ||
Der Satz des Pythagoras findet in vielen Bereichen Anwendung | Der Satz des Pythagoras findet in vielen Bereichen Anwendung. Einige davon sind im Folgenden aufgelistet. | ||
=== Längen im rechtwinkligen Dreieck === | === Längen im rechtwinkligen Dreieck === | ||
Die wohl häufigste Anwendung des Satz des Pythagoras im Schulkontext bildet die Berechnung der Seitenlängen in einem rechtiwnkligen Dreieck. Betrachte ein Dreieck wie im Bild rechts, in welchem die Seite c die Hypothenuse darstellt, dann lässt sich anhand zweier gegebener Seitenlängen mithilfe der folgenden Formeln, die sich unmittelbar aus dem Satz des Pythagoras ergeben, stets die fehlende dritte Seitenlänge berechnen. | |||
[[Datei:Formeln Berechnung.jpg|100px]] | |||
=== Euklidische Norm === | === Euklidische Norm === | ||
Version vom 25. Juli 2021, 16:30 Uhr
Der Satz des Pythagoras ist ein zentraler Satz der Geometrie. Er gilt als einer der am häufigsten bewiesenen Sätze der Mathematik. [1]
Geschichte
Mathematische Aussage
Der Satz des Pythagoras beschreibt den Zusammenhang zwischen den Seitenlängen eines rechtwinkligen Dreiecks. Formal wird der Satz dabei wie folgt formuliert:
In einem rechtwinkligen Dreieck ist der Flächeninhalt des Quadrats über der Hypotenuse gleich der Summe der Flächeninhalte der Quadrate über den Katheten.
Formal wird der Satz in Symbolsprache wie folgt formuliert:

Mathematische Anwendung
Der Satz des Pythagoras findet in vielen Bereichen Anwendung. Einige davon sind im Folgenden aufgelistet.
Längen im rechtwinkligen Dreieck
Die wohl häufigste Anwendung des Satz des Pythagoras im Schulkontext bildet die Berechnung der Seitenlängen in einem rechtiwnkligen Dreieck. Betrachte ein Dreieck wie im Bild rechts, in welchem die Seite c die Hypothenuse darstellt, dann lässt sich anhand zweier gegebener Seitenlängen mithilfe der folgenden Formeln, die sich unmittelbar aus dem Satz des Pythagoras ergeben, stets die fehlende dritte Seitenlänge berechnen.
Euklidische Norm
Pythagoreische Tripel
Beweise
Literaturverzeichnis
- ↑ Eli Maor: The Pythagorean Theorem: A 4,000-year History. Princeton University Press, Princeton 2007, ISBN 0-691-12526-0., S. XIII (Vorwort).