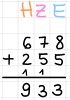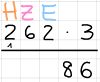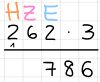Schriftliches Rechnen

Das Schriftliche Rechnen hilft beim Lösen größerer Additions-, Subtraktions-, Multiplikations- und Divisionsaufgaben. Das Rechnen soll also ohne Unterstützung eines Taschenrechners oder ähnlichem erfolgen. Dieser Beitrag befasst sich mit den Verfahren der Schriftlichen Addition, Subtraktion und Multiplikation.

Schriftliche Addition

Bei der Schriftlichen Addition werden die Zahlen so aufgeschrieben, dass Einer, Zehner, Hunderter etc. untereinander stehen. Ein Pluszeichen kommt links neben und ein Strich unter die Zahlen.

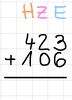
Das Rechnen beginnt immer hinten bei den Einern. Als Erstes addiert man die Einer und schreibt das Ergebnis in die Einer-Spalte unter dem Strich.

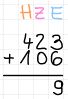
Nach den Einern guckt man sich die Zehner an, addiert diese miteinander und schreibt sie neben die Einer in die Zehner-Spalte unter dem Strich.

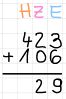
Dann macht man das Gleiche mit den Hundertern und schreibt das Ergebnis unter den Strich.

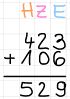
Addition mit Übertrag

Manchmal kommt es vor, dass das Ergebnis der Addition der einzelnen Stellen nicht einstellig ist. Sobald die 10 erreicht wurde, spricht man von einem Übertrag.

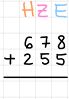
Der Einer des Ergebnisses wird erst in die jeweilige Spalte unter dem Strich geschrieben, der Zehner des Ergebnisses kommt als Übertrag in die nächste Spalte über dem Strich.

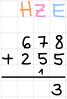
Nun addiert man die Zahlen, einschließlich Übertrag (!), miteinander und schreibt sie unter den Strich. Möglicherweise entsteht bei diesem Schritt wieder ein Übertrag. Dieser wird also wieder in die dementsprechende Spalte geschrieben.

• 
• 

Mehr als zwei Summanden

Bei mehr als zwei Summanden ist das Verfahren das Gleiche. Man addiert die Zahlen der einzelnen Stellen miteinander und gegebenenfalls schreibt man noch den Übertrag dazu.

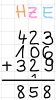
Schriftliche Subtraktion

Die Schriftliche Subtraktion ist die Umkehroperation der Schriftlichen Addition. Hierbei werden die Zahlen wieder untereinander geschrieben, der Minuend ist oben und der Subtrahend unten. Ein Minuszeichen kommt links neben und ein Strich unter die Zahlen.

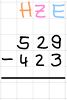
Von hinten nach vorne führt man einfache Subtraktionen durch um das Endergebnis zu erhalten.

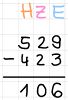
Subtraktion mit Übertrag

Ist die Ziffer des Minuenden (oben) größer als die des Subtrahenden (unten), hilft der Übertrag bei der Rechnung.

Man erweitert die Ziffer des Minuenden um 10, subtrahiert die Ziffer des Subtrahenden von der erweiterten Ziffer und addiert den Übertrag 1 zum Subtrahenden an der linksstehenden Stelle.

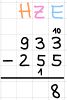
Jetzt zieht man die Ziffer mit dem addierten Übertrag 1 von der Ziffer des Minuenden ab. Ist der Minuend wieder kleiner als der Subtrahend, wiederholt sich der ganze Vorgang.

Schriftliche Multiplikation

Um die Schriftliche Multiplikation zu erleichtern, ist es besser den Faktor mit den meisten Stellen an den Anfang zu setzen. Auf diesen folgt ein Malzeichen und der zweite Faktor.

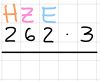
Zuerst wird der Einer des ersten Faktors mit dem zweiten Faktor multipliziert und das Ergebnis unter den zweiten Faktor unter den Strich geschrieben.

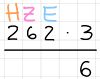
Das wiederholt sich bei den nächsten Stellen. Sollte das Produkt jedoch größer als 9 sein, entsteht ein Übertrag den man an der nächsten Stelle dazu addiert.

• 
• 

Überschlag

Mit einer Überschlagsrechnung versucht man vor der eigentlichen Rechnung grob das Endergebnis abzuschätzen. Dazu rundet man, je nachdem, auf den Zehner oder Hunderter und rechnet das Ergebnis im Kopf aus.

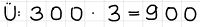
Dann rechnet man die eigentliche Multiplikationsaufgabe schriftlich aus. Nun vergleicht man das Ergebnis mit dem Ergebnis der Überschlagsrechnung und guckt, ob sie sich bezüglich der Größe naheliegen.

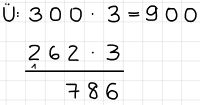
Übungsaufgaben

Berechne folgende Aufgaben schriftlich aus und überprüfe das Ergebnis mit einem Taschenrechner. Falls dir keiner zur Verfügung steht, kannst du diesen Online-Taschenrechner verwenden.

1. 312 + 599 =
2. 266 + 111 + 479 =
3. 817 - 302 =
4. 723 - 586 =
5. 499 • 2 =
6. 168 • 5 =

Quellen

1. https://www.gut-erklaert.de/mathematik/schriftlich-rechnen.html
2. https://www.gut-erklaert.de/mathematik/schriftlich-subtrahieren.html
3. https://de.bettermarks.com/mathe/schriftliche-subtraktion/
4. https://de.bettermarks.com/mathe/schriftliche-multiplikation/
5. https://www.schuelerhilfe.de/online-lernen/1-mathematik/426-ueberschlagsrechnung
6. https://www.gut-erklaert.de/mathematik/ueberschlag-mathe-multiplikation.html