Sinusfunktion
Die Sinusfunktion ist eine trigonometrische Funktion. Sie ist auffällig durch ihre Periodizität und ihre, sich zyklisch wiederholenden, Ableitungen.
Graphische Darstellung
Standardfunktion
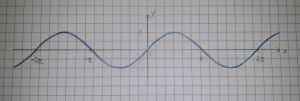
In diesem Abschnitt wird nur auf die Funktion f(x) = sin(x) eingegangen.
Die Sinusfunktion verläuft 2π-periodisch und ist punktsymmetrisch zum Koordinatenursprung. Der Definitionsbereich umfasst alle Reellen Zahlen. Der Wertebereich beschränkt sich auf alle Reellen Zahlen des Intervalls [-1,1]. Nullstellen besitzt die Funktion bei sin(kπ) mit k aus den Ganzen Zahlen. In sin(kπ+π/2) besitzt die Funktion Hochpunkte und in sin(kπ+3π/2) Tiefpunkte, wobei k aus den Ganzen Zahlen.
Einfluss von Parametern
f(x) = a * sin(bx + c)
Der Parameter a hat Einfluss auf die Amplitude des Funktionsgraphen und sorgt für die Änderung des Wertebereiches auf [-a,a].
Der Parameter b beeinflusst die Periodizität der Sinusfunktion. So ist sie dann nur 2π/b-periodisch.
Der Parameter c verursacht eine Verschiebung um (c/b) entlang der x-Achse. Für c/b > 0 gibt es eine Verschiebung nach links, für c/b < 0 eine Verschiebung nach rechts.[1]
Ableitung
Man sollte sich zunächst mit den Ableitungsregeln für Funktionen vertraut machen.
Allgemein
Besonders wichtig ist dabei die Kettenregel. Sie besagt vereinfacht: "innere mal äußere Ableitung".
Die Sinusfunktion (als äußere Funktion) besitzt, sich zyklisch wiederholende, Ableitungen.
f(x) = sin(x)
f`(x) = cos(x)
f``(x) = -sin(x)
f```(x) = -cos(x)
f^(4)(x) = sin(x)
...
Die Ableitung der inneren Funktionen müssen je nach Funktionstyp über andere Ableitungsregeln gelöst werden. Beispiele dazu folgen im nächsten Abschnitt.
Beispiele
f(x) = sin(x^2) ==> f`(x) = 2x * cos(x^2)
f(x) = sin(e^x) ==> f`(x) = e^x * cos(e^x)
f(x) = -2 * sin(3x^4) ==> f`(x) = -2 * 12x^3 * cos(3x^4) = -24x^3 * cos(3x^4)
Aufgaben
1.) Geben Sie alle Nullstellen der Funktion f(x) = sin(2x) im Intervall [0,π] an.
2.) Untersuchen Sie den Einfluss des Parameters d mit f(x) = sin(x) + d. Zeichnen Sie einen Graphen mit einem frei gewählten d und nennen Sie mögliche Änderungen des Definitions- oder Wertebereiches.
3.) Leiten Sie folgende Funktionen jeweils zweimal ab. a) f(x) = sin(3x^2 + 5x) b) g(x) = -sin(12e^x)
Quellen
- ↑ aus: Dr Engelmann, Lutz: Formeln und Tabellen für die Sekundarstufe I und II. 5. überarbeitete Auflage. Berlin, paetec Gesellschaft für Bildung und Technik mbH 1994. (S. 39)