Parallelogramm: Unterschied zwischen den Versionen
| (12 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
== Parallelogramm == | == Parallelogramm == | ||
'''Parallelogramme''' sind [[Vierecke]], bei denen die gegenüberliegenden Seiten gleich lang und parallel sind. Ein Parallelogramm wird auch als '''Rohmboid''' bezeichnet | '''Parallelogramme''' sind [[Vierecke]], bei denen die gegenüberliegenden Seiten gleich lang und parallel sind. Ein Parallelogramm wird auch als '''Rohmboid''' bezeichnet. Ein Parallelogramm hat mehrere besondere geometrische Eigenschaften. Im [[Haus der Vierecke]] steht das Parallelogramm über dem ''(allgemeinen) Trapez''. Jedes Parallelogramm ist also auch ein [[Trapez]]. | ||
== Geometrische Eigenschaften == | == Geometrische Eigenschaften == | ||
[[Datei:Parallelogramm beschriftet.png|600px|thumb|right|Winkel, Diagonale und Höhe ha der Seite a im Parallelogramm]] | |||
'''Umfang''' | '''Umfang:''' | ||
Der [[Umfang]] des Parallelogramms ergibt sich aus der Summe der vier Seitenlängen: | Der [[Umfang]] des Parallelogramms ergibt sich aus der Summe der vier Seitenlängen: | ||
u = 2a + 2b | u = 2a + 2b | ||
'''Flächeninhalt:''' | |||
'''Flächeninhalt''' | |||
Ein Parallelogramm hat den [[Flächeninhalt]] eines [[Rechteck]]s mit gleicher Seitenlänge und Höhe. Man berechnet ihn, indem die Länge einer Seite mit der dazugehörigen Höhe multipliziert wird. | Ein Parallelogramm hat den [[Flächeninhalt]] eines [[Rechteck]]s mit gleicher Seitenlänge und Höhe. Man berechnet ihn, indem die Länge einer Seite mit der dazugehörigen Höhe multipliziert wird. | ||
A = a·ha = b·hb | A = a·ha = b·hb | ||
'''Winkel''' | '''Winkel:''' | ||
Im Parallelogramm sind die gegenüberliegenden [[Winkel]] gleich groß. | Im Parallelogramm sind die gegenüberliegenden [[Winkel]] gleich groß. | ||
Die [[Summe]] zwei benachbarter [[Winkel]] (α und β) ergibt 180 Grad. | Die [[Summe]] zwei benachbarter [[Winkel]] (α und β) ergibt 180 Grad. | ||
'''Diagonalen:''' | |||
Die Diagonalen im Parallelogramm halbieren sich gegenseitig. | |||
== Übungsaufgaben == | |||
1) Ein Parallelogramm hat einen Umfang u von 20 cm. Eine Seite des Parallelogramms ist 4 cm lang. Bestimme die '''Länge der anderen Seiten'''. | |||
2) Die Seite b eines Parallelogramms ist 5 cm lang und die dazugehörende Höhe hb beträgt 3 cm. Berechne den '''Flächeninhalt''' des Parallelogramms. | |||
== Quelle == | |||
Rudolph, Dennis (2018). [https://www.gut-erklaert.de/mathematik/parallelogramm-eigenschaften-formeln.html Parallelogramm: Eigenschaften und Formeln. [20.03.2021]] | |||
[[Kategorie: Geometrie]] | [[Kategorie: Geometrie]] | ||
Aktuelle Version vom 21. März 2021, 14:02 Uhr
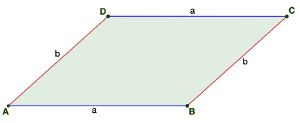
Parallelogramm
Parallelogramme sind Vierecke, bei denen die gegenüberliegenden Seiten gleich lang und parallel sind. Ein Parallelogramm wird auch als Rohmboid bezeichnet. Ein Parallelogramm hat mehrere besondere geometrische Eigenschaften. Im Haus der Vierecke steht das Parallelogramm über dem (allgemeinen) Trapez. Jedes Parallelogramm ist also auch ein Trapez.
Geometrische Eigenschaften
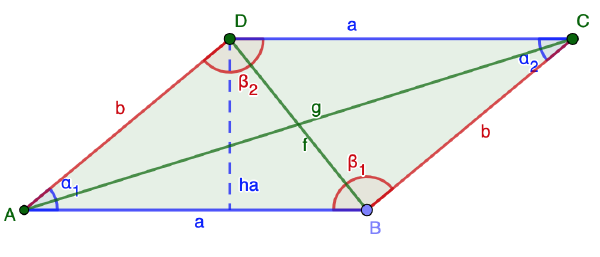
Umfang: Der Umfang des Parallelogramms ergibt sich aus der Summe der vier Seitenlängen: u = 2a + 2b
Flächeninhalt: Ein Parallelogramm hat den Flächeninhalt eines Rechtecks mit gleicher Seitenlänge und Höhe. Man berechnet ihn, indem die Länge einer Seite mit der dazugehörigen Höhe multipliziert wird. A = a·ha = b·hb
Winkel: Im Parallelogramm sind die gegenüberliegenden Winkel gleich groß. Die Summe zwei benachbarter Winkel (α und β) ergibt 180 Grad.
Diagonalen: Die Diagonalen im Parallelogramm halbieren sich gegenseitig.
Übungsaufgaben
1) Ein Parallelogramm hat einen Umfang u von 20 cm. Eine Seite des Parallelogramms ist 4 cm lang. Bestimme die Länge der anderen Seiten.
2) Die Seite b eines Parallelogramms ist 5 cm lang und die dazugehörende Höhe hb beträgt 3 cm. Berechne den Flächeninhalt des Parallelogramms.
Quelle
Rudolph, Dennis (2018). Parallelogramm: Eigenschaften und Formeln. [20.03.2021]