Bruchrechnung: Unterschied zwischen den Versionen
DiMedS (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
DiMedS (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung |
||
| (14 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
etwas darunter vorstellen zu können. | etwas darunter vorstellen zu können. | ||
Dabei werden in diesem Artikel die grundlegenden Umschreibungen zwischen den verschiedenen Schreibweisen beschrieben, | |||
während das Rechnen mit Brüchen in den weiteren Einträgen [[Addition und Subtraktion von Brüchen]] und [[Multiplikation und Division von Brüchen]] behandelt wird. | |||
Die Thematik der [[Identifizierung von Bruchzahlen]] wird in dem hinterlegten Artikel beschrieben, auf dieses Wissen wird hier aufgebaut. | |||
==Begriffsklärung== | ==Begriffsklärung== | ||
Gebrochene Zahlen können in den unterschiedlichsten Formen dargestellt werden. | Gebrochene Zahlen können in den unterschiedlichsten Formen dargestellt werden. | ||
| Zeile 10: | Zeile 14: | ||
Zum Einen gibt es die gemeinen Brüche, die unter anderem aus einem Nenner bestehen, der unter dem Bruchstrich steht und beschreibt, | Zum Einen gibt es die gemeinen Brüche, die unter anderem aus einem Nenner bestehen, der unter dem Bruchstrich steht und beschreibt, | ||
in wie viele Teile ein Ganzes aufgeteilt wird. Darüber ist ein waagerechter Bruchstrich und oben befindet sich der Zähler, | in wie viele Teile ein Ganzes aufgeteilt wird. Darüber ist ein waagerechter Bruchstrich und oben befindet sich der Zähler, | ||
der angibt, wie viele dieser Bruchteile eines Ganzen genommen werden: ÷ | der angibt, wie viele dieser Bruchteile eines Ganzen genommen werden: ÷ | ||
[[Datei:Gemeiner Bruch.PNG|mini|Gemeiner Bruch]] | |||
Die sogenannte gemischte Schreibweise kann dann genutzt werden, wenn der Zähler größer als der Nenner ist, | Die sogenannte gemischte Schreibweise kann dann genutzt werden, wenn der Zähler größer als der Nenner ist, | ||
| Zeile 16: | Zeile 22: | ||
Der ganze Teil ergibt sich durch das Teilen der nächstkleineren Zahl des Zählers, die durch den Nenner teilbar ist. | Der ganze Teil ergibt sich durch das Teilen der nächstkleineren Zahl des Zählers, die durch den Nenner teilbar ist. | ||
Der neue Zähler des übrigen Bruches ist die Differenz von altem Zähler und der nächstkleineren, durch den Nenner teilbaren Zahl: | Der neue Zähler des übrigen Bruches ist die Differenz von altem Zähler und der nächstkleineren, durch den Nenner teilbaren Zahl: | ||
1÷ | 1÷ | ||
[[Datei:Gemischte Schreibweise.PNG|mini|Gemischte Schreibweise]] | |||
Von dieser gemischten Schreibweise können die Brüche auch zurück in einen gemeinen Bruch umgeschrieben werden, indem man die ganze Zahl | Von dieser gemischten Schreibweise können die Brüche auch zurück in einen gemeinen Bruch umgeschrieben werden, indem man die ganze Zahl | ||
vor dem Bruchstrich mit dem Nenner des Bruches multipliziert, dazu den Zähler addiert und schon hat man den Zähler des gemeinen Bruches, | vor dem Bruchstrich mit dem Nenner des Bruches multipliziert, dazu den Zähler addiert und schon hat man den Zähler des gemeinen Bruches, | ||
den man nur noch auf den Nenner schreiben muss. | den man nur noch auf den Nenner schreiben muss. | ||
[[Datei:Dezimalzahl.PNG|mini|Umschreiben in eine Dezimalzahl]] | |||
Brüche können außerdem auch in eine Dezimalzahl umgeschrieben werden, indem man Zähler durch Nenner teilt, | Brüche können außerdem auch in eine Dezimalzahl umgeschrieben werden, indem man Zähler durch Nenner teilt, | ||
meist nimmt man diese Umschreibung über ein | meist nimmt man diese Umschreibung über ein Erweitern/Kürzen auf einen Nenner vor, der eine 1 und daran hängende Nullen besitzt. | ||
Anschließend schreibt man den Zähler auf und zählt von hinten so viele Nachkommastellen ab, wie der Zähler Nullen hat. | Anschließend schreibt man den Zähler auf und zählt von hinten so viele Nachkommastellen ab, wie der Zähler Nullen hat. | ||
Andersherum kann man eine Zahl auch ohne Komma als Zähler aufschreiben und als Nenner eine 1 mit so vielen Nullen, wie die Ausgangszahl | Andersherum kann man eine Zahl auch ohne Komma als Zähler aufschreiben und als Nenner eine 1 mit so vielen Nullen, wie die Ausgangszahl | ||
| Zeile 27: | Zeile 39: | ||
[[Datei:Erweitern.png|mini|Beispiel Erweitern]] | [[Datei:Erweitern.png|mini|Beispiel Erweitern]] | ||
[[Datei:Darstellung Erweitern.JPEG|mini|Erweitern bildliche Darstellung]] | |||
==Erweitern== | ==Erweitern== | ||
| Zeile 35: | Zeile 48: | ||
[[Datei:Kürzen.PNG|mini|Beispiel Kürzen]] | [[Datei:Kürzen.PNG|mini|Beispiel Kürzen]] | ||
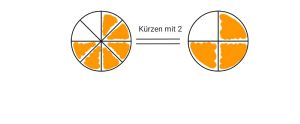
[[Datei:Darstellung Kürzen.JPEG|mini|Kürzen bildliche Darstellung]] | |||
==Kürzen== | ==Kürzen== | ||
| Zeile 42: | Zeile 56: | ||
Dafür werden beide durch denselben Divisor geteilt. | Dafür werden beide durch denselben Divisor geteilt. | ||
== | ==Übungsaufgabe== | ||
Im Folgenden wollen wir probieren, ob wir das Erweitern und Kürzen beherrschen und die Schreibweisen ineinander umformen können. | |||
Diese Fähigkeiten sind Grundlagen der Bruchrechnung und wir brauchen sie später auch für die Grundrechenarten | |||
[[Addition und Subtraktion von Brüchen]] und [[Multiplikation und Division von Brüchen]]. | |||
Darauf aufbauend können wir dann auch [[Sachaufgaben]] bearbeiten und tatsächliche alltägliche Probleme lösen. | |||
Formen Sie die folgenden Brüche in die angegebenen Brüche jeweils in einen gemeinen Bruch oder eine Dezimalzahl um:<br> | |||
a) 0,4<br> | |||
b) ¼<br> | |||
c) 2,6<br> | |||
d) ⅝ | |||
Erweitern Sie folgende Brüche mit der jeweils angegebenen Zahl<br> | |||
e) ⅛ mit 4<br> | |||
f) ⅓ mit 5<br> | |||
g) ½ mit 3 | |||
Schreiben Sie die angebebenen Brüche als gemeinen Bruch und Kürzen Sie mit der jeweils angegebenen Zahl | |||
h) 3,5 mit mit 5<br> | |||
i) vier Sechzehntel mit 4<br> | |||
j) fünf Fünfundreißigstel mit der größtmöglichen Zahl | |||
[[Category:Arithmetik]] | |||
Aktuelle Version vom 5. August 2021, 08:18 Uhr
Gebrochene Zahlen erleichtern uns das Darstellen vieler verschiedener Sachverhalte. Dieser alltagsnahe Bereich der Mathematik findet Anwendung in vielen Bereichen unseres Lebens, weshalb es sinnvoll ist, sich mit Begriffen wie drei Viertel und 1,5 auszukennen und sich vor allem etwas darunter vorstellen zu können.
Dabei werden in diesem Artikel die grundlegenden Umschreibungen zwischen den verschiedenen Schreibweisen beschrieben, während das Rechnen mit Brüchen in den weiteren Einträgen Addition und Subtraktion von Brüchen und Multiplikation und Division von Brüchen behandelt wird.
Die Thematik der Identifizierung von Bruchzahlen wird in dem hinterlegten Artikel beschrieben, auf dieses Wissen wird hier aufgebaut.
Begriffsklärung
Gebrochene Zahlen können in den unterschiedlichsten Formen dargestellt werden. Alle Formen haben gemeinsam, dass sie den Bruchteil eines Ganzen darstellen, also Element der Rationalen Zahlen ℚ sind.
Zum Einen gibt es die gemeinen Brüche, die unter anderem aus einem Nenner bestehen, der unter dem Bruchstrich steht und beschreibt, in wie viele Teile ein Ganzes aufgeteilt wird. Darüber ist ein waagerechter Bruchstrich und oben befindet sich der Zähler, der angibt, wie viele dieser Bruchteile eines Ganzen genommen werden: ÷

Die sogenannte gemischte Schreibweise kann dann genutzt werden, wenn der Zähler größer als der Nenner ist, dann kann man den Bruch in einen ganzen Teil und einen Bruchteil aufteilen. Der ganze Teil ergibt sich durch das Teilen der nächstkleineren Zahl des Zählers, die durch den Nenner teilbar ist. Der neue Zähler des übrigen Bruches ist die Differenz von altem Zähler und der nächstkleineren, durch den Nenner teilbaren Zahl: 1÷
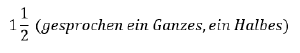
Von dieser gemischten Schreibweise können die Brüche auch zurück in einen gemeinen Bruch umgeschrieben werden, indem man die ganze Zahl vor dem Bruchstrich mit dem Nenner des Bruches multipliziert, dazu den Zähler addiert und schon hat man den Zähler des gemeinen Bruches, den man nur noch auf den Nenner schreiben muss.
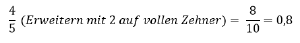
Brüche können außerdem auch in eine Dezimalzahl umgeschrieben werden, indem man Zähler durch Nenner teilt, meist nimmt man diese Umschreibung über ein Erweitern/Kürzen auf einen Nenner vor, der eine 1 und daran hängende Nullen besitzt. Anschließend schreibt man den Zähler auf und zählt von hinten so viele Nachkommastellen ab, wie der Zähler Nullen hat. Andersherum kann man eine Zahl auch ohne Komma als Zähler aufschreiben und als Nenner eine 1 mit so vielen Nullen, wie die Ausgangszahl Nachkommastellen besitzt. Durch Kürzen können wir den gemeinen Bruch noch vereinfachen.
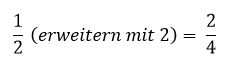
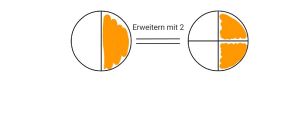
Erweitern
Das Erweitern dient dazu, gemeine Brüche in einen anderen gemeinen Bruch umzuschreiben, der zwar denselben Anteil darstellt, also per Definition gleich ist, aber durch eine Erhöhung des Nenners und Zählers beschreibt er eine feinere Zerlegung des Ganzen.
Hierbei multipliziert man sowohl Nenner, als auch Zähler mit demselben Faktor.

Kürzen
Das Kürzen von gemeinen Brüchen dient dazu, diese in je einen anderen umzuschreiben, der wieder denselben Anteil darstellt, allerdings sowohl einen geringeren Nenner, als auch Zähler besitzt.
Dafür werden beide durch denselben Divisor geteilt.
Übungsaufgabe
Im Folgenden wollen wir probieren, ob wir das Erweitern und Kürzen beherrschen und die Schreibweisen ineinander umformen können. Diese Fähigkeiten sind Grundlagen der Bruchrechnung und wir brauchen sie später auch für die Grundrechenarten Addition und Subtraktion von Brüchen und Multiplikation und Division von Brüchen. Darauf aufbauend können wir dann auch Sachaufgaben bearbeiten und tatsächliche alltägliche Probleme lösen.
Formen Sie die folgenden Brüche in die angegebenen Brüche jeweils in einen gemeinen Bruch oder eine Dezimalzahl um:
a) 0,4
b) ¼
c) 2,6
d) ⅝
Erweitern Sie folgende Brüche mit der jeweils angegebenen Zahl
e) ⅛ mit 4
f) ⅓ mit 5
g) ½ mit 3
Schreiben Sie die angebebenen Brüche als gemeinen Bruch und Kürzen Sie mit der jeweils angegebenen Zahl
h) 3,5 mit mit 5
i) vier Sechzehntel mit 4
j) fünf Fünfundreißigstel mit der größtmöglichen Zahl