Trapez

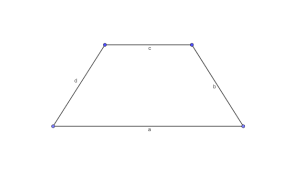
Ein Trapez ist eine Viereck, mit zwei zueinander parallelen Seiten (im Bild die Seiten a und c).

Eigenschaften

Ein Trapez ist eine ebene Fläche, bei der zwei gegenüberliegende Seiten parallel sind. Im Allgemeinen werden die beiden parallelen Seiten (im Bild a und c) als Grundseiten und die längere der beiden Grundseiten als Basis (hier a) bezeichnet. Die beiden anliegenden Seiten (hier b und c) heißen Schenkel.

Höhe h des Trapez

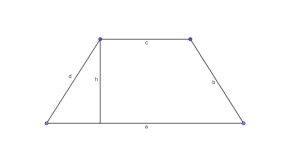
Die Höhe h eines Trapezes ist der Abstand der beiden Grundseiten.

Die Mittelparallele m liegt parallel zu den beiden Grundseiten und hat zu beiden den gleichen Abstand.

Mittelparallele m des Trapez

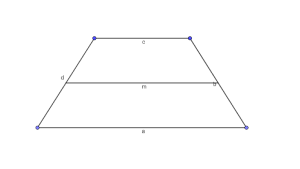
Zudem beinhaltet ein Trapez 4 Inneninkel, deren Summe 360° beträgt.

Betrachten wir das Haus der Vierecke, lassen sich folgende Aussagen ableiten:

• Jedes Quadrat ist ein Trapez
• Jede Raute ist ein Trapez
• Jedes Rechteck ist ein Trapez

Berechnungen am Trapez

Umfang eines Trapezes

Der Umfang eines Trapezes ist die Summer aller 4 Seiten.

U= a+b+c+d

Flächeninhalt eines Trapezes

Der Flächeninhalt von Trapezen kann auf zwei verschiedene Weisen berechnet werden:

• A= m᛫h
• A= 0,5᛫(a+c)᛫h

Übungsaufgaben

1) Bei einem Trapez sind folgende Größen gegeben:

• a= 5cm
• b= 3cm
• c= 4cm
• d= 2cm
• h= 1,5cm

Berechne den Umfang und den Flächeninhalt A des Trapez.

2) Bei einem Trapez sind folgende Größen gegeben:

• A= 7cm²
• a= 8cm
• c= 4cm

Berechne die Länge der Höhe h des Trapez.